


Next:
2 Concept of geometrical
Up:
Analytical Solution of
Previous:
Analytical Solution of
Shape From Shading (SFS)
problem of Lambertian reflectance model[
11
] is classified as a classical problem in nonlinear Partial Differential
Equation (PDE) of first order
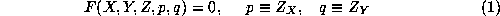
requiring the formal assumption of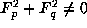 and
and continuity of
F
at each local point and in some neighborhood of this point for the
existence of solution[
17
,
21
,
20
]. This problem is interpreted geometrically, in
X
,
Y
,
Z
space, as finding the
continuity of
F
at each local point and in some neighborhood of this point for the
existence of solution[
17
,
21
,
20
]. This problem is interpreted geometrically, in
X
,
Y
,
Z
space, as finding the continuous surface
Z
(
X
,
Y
), contacted by local tangent patch which has normal vector (
p
,
q
,-1) and which satisfies eq. (
1
).
continuous surface
Z
(
X
,
Y
), contacted by local tangent patch which has normal vector (
p
,
q
,-1) and which satisfies eq. (
1
).
This problem is a widely studied one in mathematics,
physics
, and computer vision. Traditional approach based on Characteristic
Strip Expansion Method (CSEM) is already well known in differential
geometry[
22
,
23
,
12
] and PDE[
6
,
7
,
24
,
25
]. Recently, viscosity solution[
2
,
3
,
21
] and/or Level Curve Propagating Method[
19
,
20
] (LCPM) have been introduced for overcoming the defects of CSEM.
However, all these ways are basically similar in the fact of globally
propagating from a known initial condition, i.e. a non-characteristic
curve or a singular point.
Typically, in computer vision, there have been two types of numerical
approaches, optimizing approach and geometrical one, employed in the
solution of the SFS problem(see [
10
,
26
] for typical approaches). Numerous optimizing techniques for overcoming
ill-constrained nature of the problem have been tried by iteratively
minimizing a cost function which basically describes the differences
between the model and observed image. The main problem of these
approaches is that these usually require a lots of iterations without
guarantee of convergence. Geometrical approaches, a way of directly
solving this problem, have been started from CSEM[
9
], and an analysis about properties of characteristic strip has been
studied by [
17
]. Recently, the number of iterations have been considerably reduced by
introducing stable approaches based on viscosity solution[
21
] and/or LCPM[
1
,
20
,
14
].
Nevertheless, we believe that the study about uniqueness and existence
of analytical solution of SFS problem have not been fully proceeded
until now regardless of recent works[
17
,
18
,
5
,
16
]. This topic about existence and uniqueness will be discussed based on
a revised geometrical interpretation of the SFS problem by assuming
known position of light source, normalized albedo, and the orthographic
projection.
The concept of global solution and the existence of local solution will
be discussed in Sect.
2
. The continuous analytical solution will be derived in Sect.
3
, being immediately followed by discussions in Sect.
4
.
continuous analytical solution will be derived in Sect.
3
, being immediately followed by discussions in Sect.
4
.



Next:
2 Concept of geometrical
Up:
Analytical Solution of
Previous:
Analytical Solution of
Seong Ik CHO
Wed Jul 9 19:45:21 JST 1997
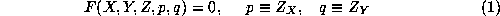
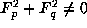 and
and continuity of
F
at each local point and in some neighborhood of this point for the
existence of solution[
17
,
21
,
20
]. This problem is interpreted geometrically, in
X
,
Y
,
Z
space, as finding the
continuity of
F
at each local point and in some neighborhood of this point for the
existence of solution[
17
,
21
,
20
]. This problem is interpreted geometrically, in
X
,
Y
,
Z
space, as finding the continuous surface
Z
(
X
,
Y
), contacted by local tangent patch which has normal vector (
p
,
q
,-1) and which satisfies eq. (
1
).
continuous surface
Z
(
X
,
Y
), contacted by local tangent patch which has normal vector (
p
,
q
,-1) and which satisfies eq. (
1
).


 continuous analytical solution will be derived in Sect.
continuous analytical solution will be derived in Sect.