


Next:
4 Discussions and conclusions
Up:
Analytical Solution of
Previous:
2 Concept of geometrical
The
direct interpretation
of the SFS problem provides the same conclusion as that of previous
section. The angle of intersection by two normal vectors is equivalent
to that by two corresponding tangent planes and
vice verse
. That is, when and
and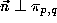 ,
,

The intersection by two planes generates a line in the direction of as is shown in Fig.
6
. The angle
as is shown in Fig.
6
. The angle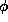 in the figure is defined by the direction of the vector
in the figure is defined by the direction of the vector which corresponds to the orthogonally projected vector of
which corresponds to the orthogonally projected vector of . The existence of this line is supported by the existence and
intersection of two planes
. The existence of this line is supported by the existence and
intersection of two planes and
and , or the existence of the SFS problem itself; and this is another
manifestation of the continuity because the tangent surface is defined
in continuous domain. Then this line is represented by a angle
, or the existence of the SFS problem itself; and this is another
manifestation of the continuity because the tangent surface is defined
in continuous domain. Then this line is represented by a angle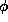 , which is another presentation of the vector
, which is another presentation of the vector ; where the angle
; where the angle is that of the vector
is that of the vector . These two angles which are independent each other satisfy eq. (
2
) simultaneously, and hence these constrain the problem orthogonally.
This is same conclusion as that of Sect.
2.2
.
. These two angles which are independent each other satisfy eq. (
2
) simultaneously, and hence these constrain the problem orthogonally.
This is same conclusion as that of Sect.
2.2
.
The stable value of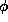 at each pixel position on a digital image can be determined by fitting
the brightness distribution of neighboring pixels into bi-linear or
higher order distribution function. For example, bi-linear approximation
function
G
(
X
,
Y
) is described as
at each pixel position on a digital image can be determined by fitting
the brightness distribution of neighboring pixels into bi-linear or
higher order distribution function. For example, bi-linear approximation
function
G
(
X
,
Y
) is described as

where (
X
,
Y
) denotes the position of central pixel, the mean value of neighboring pixels, and
the mean value of neighboring pixels, and the resultant error of fitting which should be minimized[
8
]. The angle
the resultant error of fitting which should be minimized[
8
]. The angle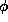 , described by
, described by , is defined along the clock-wise direction by fixing the direction of
brightness variation outward from the high (H) to the low(L) as is shown
in Fig.
7
in order to assign unique orientation of the vector
, is defined along the clock-wise direction by fixing the direction of
brightness variation outward from the high (H) to the low(L) as is shown
in Fig.
7
in order to assign unique orientation of the vector .
.
The general equation of this line is then described as

and the equations of two planes and
and are, respectively, described as
are, respectively, described as

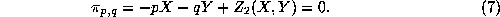
The subtraction of eq. (
7
) from eq. (
6
) becomes

because at the center of each pixel.
at the center of each pixel.
The general linear relation between
p
and
q
is then derived from eqs. (
5
) and (
8
)

This indicate that
p
and
q
are linearly connected because these are constrained by the equation of
plane, i.e. by eq. (
7
).
The solution then can be derived w.r.t. the general case and special
cases.
1) General case when (
N
: integer)
(
N
: integer)
After rewriting eq. (
9
) into

and after assigning , new form of eq. (
2
) becomes
, new form of eq. (
2
) becomes

By substituting eq. (
10
) into eq. (
11
) for the elimination of
p
and by solving the resultant equation w.r.t.
q
, the following set of analytical solutions having two degrees of
freedom is derived

where

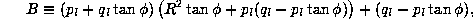

Let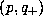 be the positive solution represented by
be the positive solution represented by =(
B
+
=(
B
+ , and
, and be another one by negative sign; then
be another one by negative sign; then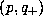 and
and correspond to convex and concave solution of surface when the over-head
light source is used.
correspond to convex and concave solution of surface when the over-head
light source is used.
2) Special cases
a) When (
N
: even integer)
(
N
: even integer)
Equation (
9
) is satisfied only when
p
=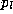 because
because =1 and
=1 and = 0. The solution becomes
= 0. The solution becomes

b) When (
N
: odd integer)
(
N
: odd integer)
In the same way,
q
= because
because =0 and
=0 and = 1. The solution becomes
= 1. The solution becomes

c) When = 1, that is at classical singular point
= 1, that is at classical singular point
Because in eq. (
12
)
A
,
B
and
D
become, respectively,

the non-singular solution which is consistent with the intuitive result
becomes

d) When =0, that is in occluding boundary
=0, that is in occluding boundary
When (
N
: odd integer), using
(
N
: odd integer), using = 0 and eq. (
10
)
= 0 and eq. (
10
)

When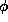 =
= (
N
: odd integer), using the fact that
q
=
(
N
: odd integer), using the fact that
q
= and eq. (
10
)
and eq. (
10
)

e) When =
=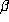 =0 in eq. (
4
)
=0 in eq. (
4
)
This corresponds to the special case that the surface is locally a
plane, that is both the principal curvatures and
and are identically zero. The solution of this point should be interpolated
from other points having the analytical solution because the solution is
not exist by our approach.
are identically zero. The solution of this point should be interpolated
from other points having the analytical solution because the solution is
not exist by our approach.
The derived solutions exist at every point of image when the surface is
not a plane locally. That is, these are analytical solutions, and
neither iteration nor global propagation starting from a special
condition is needed. Therefore, we believe that the proposed scheme is
superior to conventional approaches. The uniqueness of solution is
guaranteed only at classical singular points, which are not singular in
actual, and in occluding boundary; therefore there generally exist two
independent solutions which are ambiguous due to the non-linear property
of the SFS problem. The solutions are weak because these are basically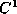 continuous w.r.t.
continuous w.r.t. continuous surface; therefore the solutions cause topological problem in
the integration process[
15
] at critical points when the role of convex/concave w.r.t. the position
of light source is switched.
continuous surface; therefore the solutions cause topological problem in
the integration process[
15
] at critical points when the role of convex/concave w.r.t. the position
of light source is switched.



Next:
4 Discussions and conclusions
Up:
Analytical Solution of
Previous:
2 Concept of geometrical
Seong Ik CHO
Wed Jul 9 19:45:21 JST 1997
 and
and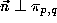 ,
,
 as is shown in Fig.
6
. The angle
as is shown in Fig.
6
. The angle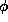 in the figure is defined by the direction of the vector
in the figure is defined by the direction of the vector which corresponds to the orthogonally projected vector of
which corresponds to the orthogonally projected vector of . The existence of this line is supported by the existence and
intersection of two planes
. The existence of this line is supported by the existence and
intersection of two planes and
and , or the existence of the SFS problem itself; and this is another
manifestation of the continuity because the tangent surface is defined
in continuous domain. Then this line is represented by a angle
, or the existence of the SFS problem itself; and this is another
manifestation of the continuity because the tangent surface is defined
in continuous domain. Then this line is represented by a angle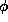 , which is another presentation of the vector
, which is another presentation of the vector ; where the angle
; where the angle is that of the vector
is that of the vector . These two angles which are independent each other satisfy eq. (
2
) simultaneously, and hence these constrain the problem orthogonally.
This is same conclusion as that of Sect.
2.2
.
. These two angles which are independent each other satisfy eq. (
2
) simultaneously, and hence these constrain the problem orthogonally.
This is same conclusion as that of Sect.
2.2
.



 the mean value of neighboring pixels, and
the mean value of neighboring pixels, and the resultant error of fitting which should be minimized[
the resultant error of fitting which should be minimized[ , is defined along the clock-wise direction by fixing the direction of
brightness variation outward from the high (H) to the low(L) as is shown
in Fig.
, is defined along the clock-wise direction by fixing the direction of
brightness variation outward from the high (H) to the low(L) as is shown
in Fig.

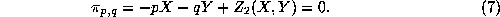

 at the center of each pixel.
at the center of each pixel.
 (
N
: integer)
(
N
: integer)

 , new form of eq. (
, new form of eq. (


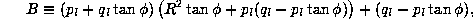

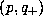 be the positive solution represented by
be the positive solution represented by =(
B
+
=(
B
+ , and
, and be another one by negative sign; then
be another one by negative sign; then (
N
: even integer)
(
N
: even integer) because
because =1 and
=1 and = 0. The solution becomes
= 0. The solution becomes
 because
because
 = 1, that is at classical singular point
= 1, that is at classical singular point

 = 0 and eq. (
= 0 and eq. (
 (
N
: odd integer), using the fact that
q
=
(
N
: odd integer), using the fact that
q
=
 =
=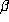 =0 in eq. (
=0 in eq. ( and
and are identically zero. The solution of this point should be interpolated
from other points having the analytical solution because the solution is
not exist by our approach.
are identically zero. The solution of this point should be interpolated
from other points having the analytical solution because the solution is
not exist by our approach.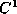 continuous w.r.t.
continuous w.r.t. continuous surface; therefore the solutions cause topological problem in
the integration process[
continuous surface; therefore the solutions cause topological problem in
the integration process[