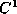We discussed the concept of a new geometrical approach in solving the
SFS problem and derived the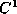
continuous weak analytical solutions of this problem.
Several ad hoc constraints have been used in numerous approaches by
assuming that the SFS problem is ill-constrained. However, we showed
that this problem is bound by at least two constraints, two angles
and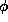
, which come from the definition of the problem itself and which is
conceptually supported by previous works in LCPM, and that the
constraints are orthogonal each other. Consequently, our work indicates
that ad hoc constraints will be needless. For example, the constraint of
occluding boundary[
13
] is just a natural result of the analytical solution as was shown and
as has been pointed out by a previous research[
18
]. It is already known that several constraints, classified as a sort of
smoothness constraints, cause over-smoothed results in some cases. This
corresponds to a typical mathematical fault which solves a problem by
using non-orthogonal constraints because the smoothness or the
continuity already constrains the problem by assuming the existence of
local slopes, i.e. that of the problem itself, which are defined on
smoothly varying domain. Whereas, we resolved the assumption of the
problem and showed that the problem is composed of two orthogonal
constraints.
We showed that a set of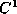
continuous analytical solutions exists at any point of a digital image
even at classical singular points and in occluding boundaries. This
proves the existence of solution. The solution is weak because the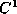
continuous solution is obtained w.r.t. the
continuous surface. The weakness causes a combination and topology
problem in the integration process[
15
]; i.e. we should select one prefer solution, using the condition of
continuity and using another assumption about convexity or concavity of
object, between two possible combinations: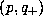
and
. This indicate that the SFS problem is not unique but has two degrees
of freedom due to the non-linear property of the problem.
We believe that the derivation of this analytical solution has
significant meaning in the fact that this solution makes it possible to
calculate the tangent surface of object using shade information fastly
and reliably without doing iteration when constant albedo of surface is
already known. The proposed geometrical concept can be applied to the
method of two-image photometric stereo for the shape recovery of object
having three unknown parameters:
p
,
q
and albedo
which is non-constant globally. This is because the SFS problem is
composed of two constraints.
In our previous research[ 4 ], it has been shown that the shape recovery problem of a cylindrical object in real environment can be solved directly using two shade images. Further researches shall be done in the shape recovery of general objects using two shade images by combining the idea of the previous and that of this research.
Seong Ik CHO