


Next:
3 Derivation of analytical
Up:
Analytical Solution of
Previous:
1 Introduction
Let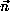 defined by (
p
,
q
,-1) be the normal vector of a point (
X
,
Y
,
Z
) existing on
defined by (
p
,
q
,-1) be the normal vector of a point (
X
,
Y
,
Z
) existing on continuous and compact surface,
continuous and compact surface, defined by
defined by -1) the position vector of a light source, then, Lambertian reflectance
-1) the position vector of a light source, then, Lambertian reflectance is described as
is described as

where denotes the angle intersected by
denotes the angle intersected by and
and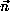 . The purpose of SFS approach is to recover the surface
Z
(
X
,
Y
), or exactly the tangent surface of
Z
(
X
,
Y
), using
. The purpose of SFS approach is to recover the surface
Z
(
X
,
Y
), or exactly the tangent surface of
Z
(
X
,
Y
), using and existing constraint(s).
and existing constraint(s).
As has been discussed in previous researches[
1
,
20
,
14
], there exist a parameter-family of planes having equal height in the direction of light source due to the constant
angle
having equal height in the direction of light source due to the constant
angle on each plane as is shown in Fig.
1
. The edge of continuous surface cut by a equal height plane becomes a
continuously connected spatial curve, i.e. the level curve. Each level
curve has a corresponding iso-intensity contour on projected image plane
(Fig.
1
). At each point (
X
,
Y
,
Z
), a tangent vector
on each plane as is shown in Fig.
1
. The edge of continuous surface cut by a equal height plane becomes a
continuously connected spatial curve, i.e. the level curve. Each level
curve has a corresponding iso-intensity contour on projected image plane
(Fig.
1
). At each point (
X
,
Y
,
Z
), a tangent vector of level curve, another vector
of level curve, another vector existing in the direction of steepest descent/ascent variation of depth,
and the normal vector
existing in the direction of steepest descent/ascent variation of depth,
and the normal vector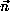 constitute locally orthogonal coordinate system; and vectors
constitute locally orthogonal coordinate system; and vectors and
and define corresponding tangent patch. Classical CSEM is a way which
recovers the tangent surface in the direction of
define corresponding tangent patch. Classical CSEM is a way which
recovers the tangent surface in the direction of [
17
]. Whereas LCPM is another way which expands level curves in the
direction of
[
17
]. Whereas LCPM is another way which expands level curves in the
direction of by curvature dependent speed of time for the recovery of tangent
surface[
20
,
14
].
by curvature dependent speed of time for the recovery of tangent
surface[
20
,
14
].
Regardless of the ways of propagation, we should rely on a constraint:
the angle . Then the solution of
. Then the solution of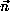 determined using
determined using and
and becomes a ambiguous cone at each point (
X
,
Y
,
Z
)[
14
]. Consequently, the solution of
becomes a ambiguous cone at each point (
X
,
Y
,
Z
)[
14
]. Consequently, the solution of becomes another cone as is shown in Fig.
2
. This cone, generated by
becomes another cone as is shown in Fig.
2
. This cone, generated by which contacts the tangent surface, is called the
Monge
cone (see pp.24-33 of [
7
] for detail). A cone is composed of stacked circles, and a family of
circles having their center on a continuous curve is contacted by two
envelop curves as is shown in Fig.
3
. A family of circles, when each circle is a sliced edge of Monge cone,
is contacted by a family of envelop curves at a proportionally given
distance from the center of each cone. Since each cone has non-zero
length determined by the length of normal vector, the stack of envelop
curves becomes a paired family of envelop surfaces having angle
which contacts the tangent surface, is called the
Monge
cone (see pp.24-33 of [
7
] for detail). A cone is composed of stacked circles, and a family of
circles having their center on a continuous curve is contacted by two
envelop curves as is shown in Fig.
3
. A family of circles, when each circle is a sliced edge of Monge cone,
is contacted by a family of envelop curves at a proportionally given
distance from the center of each cone. Since each cone has non-zero
length determined by the length of normal vector, the stack of envelop
curves becomes a paired family of envelop surfaces having angle of separation by the definition of the Monge cone. The envelop surfaces
are the solution of this SFS problem as is shown in Fig.
4
because each envelop surface, at all point of a level curve, satisfies
the condition of all Monge cones, i.e. the solution of eq. (
2
), simultaneously.
of separation by the definition of the Monge cone. The envelop surfaces
are the solution of this SFS problem as is shown in Fig.
4
because each envelop surface, at all point of a level curve, satisfies
the condition of all Monge cones, i.e. the solution of eq. (
2
), simultaneously.
Typically two tangent surfaces can be obtained between two adjacent
planes of level curves. The integration of one set of tangent surfaces
generally gives unique solution of continuous surface
Z
(
X
,
Y
) in LCPM when there is no topological change because the freedom of
selecting the orientation of three vectors doesn't change the shape of integrated surface although it changes the
propagating direction, downward or upward, of level curves. However, it
is distinct that we always have two possible solutions of resultant
surface as already discussed in [
1
,
17
] because the distinguishability of correct solution between two is not
guaranteed. Generally, the existence of the solution at singular points
and in occluding boundary is not guaranteed by the global approach[
21
,
20
].
doesn't change the shape of integrated surface although it changes the
propagating direction, downward or upward, of level curves. However, it
is distinct that we always have two possible solutions of resultant
surface as already discussed in [
1
,
17
] because the distinguishability of correct solution between two is not
guaranteed. Generally, the existence of the solution at singular points
and in occluding boundary is not guaranteed by the global approach[
21
,
20
].
The existence of global solution comes from the compact existence of
Monge cones on a level curve. This means that the SFS problem is bound
by two constraints, i.e. the intersection angle and the continuity, not by one constraint.
and the continuity, not by one constraint.
A local tangent patch, defined by the envelop surface of at least two
Monge cones, exists at any point on a level curve due to the continuity
of this curve. As is shown in Fig.
5
, this patch has angle
has angle of intersection w.r.t. the plane
of intersection w.r.t. the plane which is bound by this curve. This is a local interpretation of the
global concept of solution. Therefore, each patch
which is bound by this curve. This is a local interpretation of the
global concept of solution. Therefore, each patch is constrained by angle
is constrained by angle which can be determined from eq. (
2
), by
X
,
Y
position, and by a iso-intensity curve which corresponds to the
projected curve of each level curve. The direction of
which can be determined from eq. (
2
), by
X
,
Y
position, and by a iso-intensity curve which corresponds to the
projected curve of each level curve. The direction of , which can be obtained from this iso-intensity curve, first fixes the
axis of rotation of a tangent patch; then this patch is rotated w.r.t.
the plane
, which can be obtained from this iso-intensity curve, first fixes the
axis of rotation of a tangent patch; then this patch is rotated w.r.t.
the plane by this axis to the amount of angle
by this axis to the amount of angle . This rotation provides unique existence of local solution having two
degrees of freedom.
. This rotation provides unique existence of local solution having two
degrees of freedom.
Although the patch is constrained by the plane
is constrained by the plane , it doesn't mean that the corresponding normal vector
, it doesn't mean that the corresponding normal vector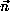 is variant w.r.t. the variation of
is variant w.r.t. the variation of . The variants are both the angle
. The variants are both the angle and the direction of
and the direction of , i.e. the level curve, because the geometrical relation between
, i.e. the level curve, because the geometrical relation between and
and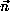 determines the level curves in the process of shading. The vector
determines the level curves in the process of shading. The vector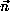 is invariant, and consequently the integrated surface is invariant as
well; and which satisfies the conservation law of Hamilton-Jacobi
equations[
2
,
20
].
is invariant, and consequently the integrated surface is invariant as
well; and which satisfies the conservation law of Hamilton-Jacobi
equations[
2
,
20
].



Next:
3 Derivation of analytical
Up:
Analytical Solution of
Previous:
1 Introduction
Seong Ik CHO
Wed Jul 9 19:45:21 JST 1997
 defined by (
p
,
q
,-1) be the normal vector of a point (
X
,
Y
,
Z
) existing on
defined by (
p
,
q
,-1) be the normal vector of a point (
X
,
Y
,
Z
) existing on continuous and compact surface,
continuous and compact surface, defined by
defined by -1) the position vector of a light source, then, Lambertian reflectance
-1) the position vector of a light source, then, Lambertian reflectance is described as
is described as
 denotes the angle intersected by
denotes the angle intersected by and
and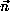 . The purpose of SFS approach is to recover the surface
Z
(
X
,
Y
), or exactly the tangent surface of
Z
(
X
,
Y
), using
. The purpose of SFS approach is to recover the surface
Z
(
X
,
Y
), or exactly the tangent surface of
Z
(
X
,
Y
), using and existing constraint(s).
and existing constraint(s).


 having equal height in the direction of light source due to the constant
angle
having equal height in the direction of light source due to the constant
angle of level curve, another vector
of level curve, another vector existing in the direction of steepest descent/ascent variation of depth,
and the normal vector
existing in the direction of steepest descent/ascent variation of depth,
and the normal vector . Then the solution of
. Then the solution of of separation by the definition of the Monge cone. The envelop surfaces
are the solution of this SFS problem as is shown in Fig.
of separation by the definition of the Monge cone. The envelop surfaces
are the solution of this SFS problem as is shown in Fig. doesn't change the shape of integrated surface although it changes the
propagating direction, downward or upward, of level curves. However, it
is distinct that we always have two possible solutions of resultant
surface as already discussed in [
doesn't change the shape of integrated surface although it changes the
propagating direction, downward or upward, of level curves. However, it
is distinct that we always have two possible solutions of resultant
surface as already discussed in [ has angle
has angle . This rotation provides unique existence of local solution having two
degrees of freedom.
. This rotation provides unique existence of local solution having two
degrees of freedom.