


Next:
4 Results
Up:
Selection for Gamut
Previous:
2 Gamut Mapping Colour
The final step in solving for colour constancy is to choose one mapping
from the set of feasible maps to represent the unknown illuminant. One
way of doing this [
4
] is to find the map that takes all image colours into the canonical
gamut such that image colours are made as colourful as possible (this is
achieved by finding the maximum area feasible map). A second approach
due to Barnard [
1
] is to assume that all mappings have an equal probability of being
correct. It is then natural to take the mean (expected) value of the
mapping set as our choice of mapping. However neither of these selection
methods is appropriate since gamut mapping has been carried out in a
non-linear perspective colour space
To illustrate this consider the situation where the correct mapping in 3
dimensions is (1, 1, 1), and that the set of possible solutions lie on a
straight line between (3, 2, 1) and (1, 2, 3). The mean vector of this
3-dimensional
solution set is (2,2,2) which in this case is a scaling from the correct
answer (which is fine since we have argued earlier that we can only
recover the illuminant up to a scalar). Under a perspective transform
the correct answer becomes (1, 1) and the possible solutions fall on the
straight line between (3, 2) and (1/3, 2/3). The maximum area and 2-d
mean for this mapping set are (3,2) and (5/3,4/3) which are quite far
from the correct answer: (1,1). It is clear that the perspective
transform has introduced an unwanted distortion into the mapping set and
nether the maximum or mean estimations are appropriate.
To avoid this bias at the selection stage we need to reconstruct the
full 3-dimensions of the mapping set (since in the above example a
mean-estimator on 3-dimensional maps was seen to work well). A
perspective map can be converted to a three vector
can be converted to a three vector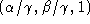 (remember the mapping set lies in the plane
(remember the mapping set lies in the plane ). We can then construct a cone with vertex at the origin and rays
passing through the extreme points of the mapping set in the plane
). We can then construct a cone with vertex at the origin and rays
passing through the extreme points of the mapping set in the plane . This cone bounds the possible variation in orientation of our feasible
maps. To select a map from this cone of feasible maps we again assume
that all maps are equally likely and take as our choice of mapping the
mean map. The cone-based mean computation is contrasted with the
perspective computation in Figure 1.
. This cone bounds the possible variation in orientation of our feasible
maps. To select a map from this cone of feasible maps we again assume
that all maps are equally likely and take as our choice of mapping the
mean map. The cone-based mean computation is contrasted with the
perspective computation in Figure 1.

Figure 1:
The dotted convex polygon denotes the gamut of feasible mappings
calculated by perspective gamut mapping. This polygon lies on the plane . The corresponding 3-dimensional cone, drawn with solid rays emanating
from the origin, bounds the mapping set post-inversion of the
perspective transform. The mean of the perspective gamut of mappings
(solid triangle) is quite different from the mean calculated in
3-dimensions (solid circle).
. The corresponding 3-dimensional cone, drawn with solid rays emanating
from the origin, bounds the mapping set post-inversion of the
perspective transform. The mean of the perspective gamut of mappings
(solid triangle) is quite different from the mean calculated in
3-dimensions (solid circle).
Calculating the mean of a set in three dimensions involves calculating
the following integrals:

where
V
is the volume of the set and
D
is the boundary of the cone. Note that every ,
, and
and corresponds to a plausible diagonal map. Of course, we must be careful
in how we carry out the computation since the cone of possible mappings
stretches to infinity: the map (1,1,1) is treated no differently from
(100,100,100) or (1000,1000,1000). Thus we must bound the size (length)
of the maps. This is done by intersecting the cone, shown in Figure
1
above, with the unit sphere.
corresponds to a plausible diagonal map. Of course, we must be careful
in how we carry out the computation since the cone of possible mappings
stretches to infinity: the map (1,1,1) is treated no differently from
(100,100,100) or (1000,1000,1000). Thus we must bound the size (length)
of the maps. This is done by intersecting the cone, shown in Figure
1
above, with the unit sphere.
To calculate (
10
) analytically turns out to be quite difficult due to the nature of the
boundary constraints (convex cone intersected with unit sphere) and so
instead we use the method of Monte Carlo integration to find an
approximate solution. Essentially this involves randomly generating
triplets of 3 numbers and calculating the proportion that fall inside
the calculated constraint cone and the unit sphere. As the number of
random vectors chosen increases, this average value approaches the mean
of the cone. A similar method is employed to find the mean in two
dimensions.



Next:
4 Results
Up:
Selection for Gamut
Previous:
2 Gamut Mapping Colour
Adrian F Clark
Thu Jul 10 22:05:37 BST 1997
 can be converted to a three vector
can be converted to a three vector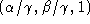 (remember the mapping set lies in the plane
(remember the mapping set lies in the plane ). We can then construct a cone with vertex at the origin and rays
passing through the extreme points of the mapping set in the plane
). We can then construct a cone with vertex at the origin and rays
passing through the extreme points of the mapping set in the plane . This cone bounds the possible variation in orientation of our feasible
maps. To select a map from this cone of feasible maps we again assume
that all maps are equally likely and take as our choice of mapping the
mean map. The cone-based mean computation is contrasted with the
perspective computation in Figure 1.
. This cone bounds the possible variation in orientation of our feasible
maps. To select a map from this cone of feasible maps we again assume
that all maps are equally likely and take as our choice of mapping the
mean map. The cone-based mean computation is contrasted with the
perspective computation in Figure 1.




 ,
, and
and corresponds to a plausible diagonal map. Of course, we must be careful
in how we carry out the computation since the cone of possible mappings
stretches to infinity: the map (1,1,1) is treated no differently from
(100,100,100) or (1000,1000,1000). Thus we must bound the size (length)
of the maps. This is done by intersecting the cone, shown in Figure
corresponds to a plausible diagonal map. Of course, we must be careful
in how we carry out the computation since the cone of possible mappings
stretches to infinity: the map (1,1,1) is treated no differently from
(100,100,100) or (1000,1000,1000). Thus we must bound the size (length)
of the maps. This is done by intersecting the cone, shown in Figure