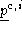 . Imaging
n
surfaces gives us a set:
. Imaging
n
surfaces gives us a set:


The image of a flat Mondrian (a Mondrian is a patchwork of matte
reflectances) viewed under unknown lighting conditions forms the input
to Forsyth's gamut mapping algorithm. From this input data we want to
recover an estimate of the unknown illuminant. We begin by constructing
the canonical gamut. This is defined to be the set of all sensor
responses obtained by viewing all physically realisable surface
reflectances under a canonical illuminant. Each surface
i
imaged under the canonical illuminant
c
produces an
rgb
sensor response represented as the 3-vector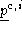 . Imaging
n
surfaces gives us a set:
. Imaging
n
surfaces gives us a set:
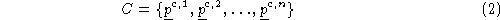
of camera responses. Since each represents the
rgb
response of the camera to a physically realisable surface, any convex
combination,
represents the
rgb
response of the camera to a physically realisable surface, any convex
combination, of vectors in
C
is also physically realisable:
of vectors in
C
is also physically realisable:
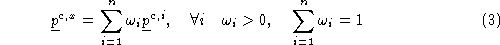
So, we take our canonical gamut to be the set of all convex combinations
of vectors in
C
, denoted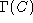 .
.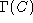 is infinite but since it is convex we need consider only its convex
hull, defined to be [
12
] the minimal cardinality subset of
C
, denoted
is infinite but since it is convex we need consider only its convex
hull, defined to be [
12
] the minimal cardinality subset of
C
, denoted , such that
, such that .
.
We next construct the image gamut where
where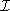 is the set of convex hull points of the
rgb
's obtained by imaging a small set of surface reflectances under an
unknown illuminant. The gamuts
is the set of convex hull points of the
rgb
's obtained by imaging a small set of surface reflectances under an
unknown illuminant. The gamuts and
and taken together, provide sufficient constraint for solving relation (1)
(the set of mappings that take
taken together, provide sufficient constraint for solving relation (1)
(the set of mappings that take inside
inside is the gamut mapping solution to colour constancy). Let the
u
th point in
is the gamut mapping solution to colour constancy). Let the
u
th point in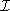 can be mapped to the
v
th point in
can be mapped to the
v
th point in by applying a diagonal matrix
by applying a diagonal matrix such that:
such that:
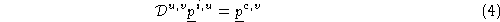

We denote the set of diagonal mappings taking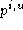 into
into as
as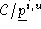 , and representing the diagonal matrices as 3-vectors we have
, and representing the diagonal matrices as 3-vectors we have
So the points in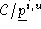 are those points in
are those points in mapped by the diagonal transform
D
. Therefore
mapped by the diagonal transform
D
. Therefore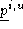 can be mapped to any point in
can be mapped to any point in by a convex combination of vectors in
by a convex combination of vectors in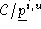 . We denote the set of all such convex combinations
. We denote the set of all such convex combinations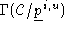 .
.
It follows then that the set of diagonal matrices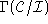 that map all the points in
that map all the points in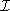 into
into is the intersection of all the sets which take a single point in
is the intersection of all the sets which take a single point in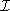 into
into :
:
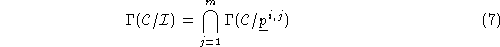
Under the world conditions imposed by Forsyth, his CRULE algorithm delivers an accurate characterisation of the solution set for colour constancy. In real images however the algorithm is less effective. Real scenes are complicated by factors, such as specularities, varying illumination and shape, that break the assumption of linear illuminant change. Finlayson [ 4 ] recognised however, that though these factors prevent accurate recovery of the illuminant intensity they do not affect recovery of the orientation of the illuminant vector in rgb space. He therefore proposed an algorithm to recover only the orientation of the illuminant vector, reducing a three dimensional problem to a simpler two dimensional one.
Finlayson ignores intensity information by mapping the 3-d rgb vectors to 2-d perspective chromaticity values. If a colour is represented by a 3-vector ( r , g , b ), then its perspective chromaticity co-ordinates are calculated as
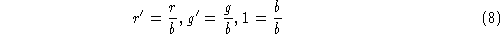
This produces a vector ( r ', g ', 1) in the same direction as ( r , g , b ) but with a different intensity. And since the third co-ordinate is always 1 we can represent these new vectors as 2-vectors ( r ', g '). An important feature of the perspective transform is that gamut convexity is preserved[ 4 ].
Perspective diagonal matrices are formed in an analogous manner to forming perspective colours:
Because diagonal matrices map perspective colours between illuminants, it is possible to run Forsyth's CRULE algorithm directly on the 2-dimensional perspective colours. Again, this algorithm produces a set of feasible mappings from which we must choose one. The question of which one to choose is addressed in the next section.



Adrian F Clark