


Next:
6 Discussion and conclusion
Up:
5 Experiments
Previous:
5.1 The tetrahedron
This object contains sets of parallel planes. The prototype objects is
composed of seven faces. We have studied the case when five faces are
visible (Fig.
3
a). For this view we have assigned a single normal for each set of
parallel planes. By this way three normals are associated respectively to surfaces (
are associated respectively to surfaces (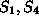 ), (
), ( ), and
), and . Besides the three angle constraints (orthogonality of each two
vectors) and the three unit constraints, this object involves as well
two distance constraints related to the fixed distances between
. Besides the three angle constraints (orthogonality of each two
vectors) and the three unit constraints, this object involves as well
two distance constraints related to the fixed distances between and
and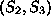 . The surfaces' points have been corrupted with a Gaussian noise of
2 mm
variance. Using equations (
5
),(
6
) and (
20
) the least squares function is:
. The surfaces' points have been corrupted with a Gaussian noise of
2 mm
variance. Using equations (
5
),(
6
) and (
20
) the least squares function is:




Figure 3:
(a) the stepmodel object. (b) decrease of the constraint error function
related to one plane normal. (c) orientation error related to one
surface normal in function of

Figure 4:
Variation of the angle constraint error related to all along the four steps of the algorithm
optim2
all along the four steps of the algorithm
optim2
The first series of tests have been carried out with the algorithm
optim1
in which all the constraints are applied simultaneously. Some results
are shown in Fig.
3
(b,c).
In the second series of experiments, the algorithm
optim2
was applied. According to this algorithm, the constraint function
changes each time a new constraint is added. Normally the incremental
process contains six steps, however since the unit constraints are used
mainly to avoid the null solution there is no need to apply them
incrementally, instead they are inferred at once simultaneously in a
single step. Thus the algorithm will comprises four steps, in the first
the unit constraints are considered, afterwards the three angle
constraints are inferred one by one. Some results are illustrated in
Fig.
4
and Fig.
5
.
Results similar to the tetrahedron case were obtained in both algorithms
for the unit constraint, the angle constraint, the least squares
function and the constraint function. Comparison of Fig.
3
b and Fig.
4
shows that the angle constraint is well satisfied in the two algorithms.
This synthetic example allows the comparison of the estimated surfaces'
normals to the actual ones. Fig.
3
c and Fig.
5
shows that the estimated vectors in each of the two algorithms are very
close to the actual ones, however we observe that the normal orientation
error is reduced by more than 100 in the second algorithm. This fact
shows that the estimated solution moves toward the actual one, and it is
almost completely reached. So we can say the optimization technique
satisfies the constraints while improving the localization to a high
degree.

Figure 5:
Variation of the orientation error related to along the four steps
along the four steps



Next:
6 Discussion and conclusion
Up:
5 Experiments
Previous:
5.1 The tetrahedron
Naoufel Werghi
Thu Jul 10 17:36:04 BST 1997
 are associated respectively to surfaces (
are associated respectively to surfaces (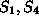 ), (
), ( ), and
), and . Besides the three angle constraints (orthogonality of each two
vectors) and the three unit constraints, this object involves as well
two distance constraints related to the fixed distances between
. Besides the three angle constraints (orthogonality of each two
vectors) and the three unit constraints, this object involves as well
two distance constraints related to the fixed distances between and
and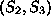 . The surfaces' points have been corrupted with a Gaussian noise of
2 mm
variance. Using equations (
5
),(
6
) and (
20
) the least squares function is:
. The surfaces' points have been corrupted with a Gaussian noise of
2 mm
variance. Using equations (
5
),(
6
) and (
20
) the least squares function is:








 all along the four steps of the algorithm
optim2
all along the four steps of the algorithm
optim2

 along the four steps
along the four steps