To avoid unnecessarily complicated algebra the comparison between first
and second order analysis is developed for a line to line homography.
The one-dimensional case illustrates all the ideas involved, and the
algebraic expressions are easily interpreted. The generalisation to
matrices is straightforward and does not provide any new insights here.
This simpler case is modelled by a homogeneous
matrix as described in section
2.1
. Under back-projection an image point
x
maps as
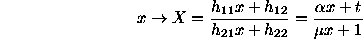
This non-linear mapping (on inhomogeneous coordinates) can be expanded
in a Taylor series. Statistical moments of
X
, such as the variance, are then computed in terms of the Taylor
coefficients and the moments of
x
[
3
,
]. It is assumed here that the homography is exact (no errors) and the
measurement of the image test point
x
is subject to Gaussian noise with standard deviation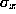
. The Taylor series is developed about the point's mean position denoted
as
.
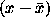then the mapping is linearised. The variance of
X
can be shown to be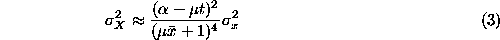
Usually only the first order approximation is used for error propagation [
2
,
4
,
5
,
10
,
11
]. Here we extend the Taylor expansion to second order so that the
approximation involved in truncating to first order can be bounded. It
can be shown that to second order in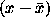
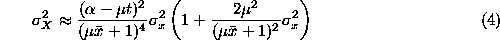
We now define two measures that can be used to assess the error in
truncating to first order. The first measures the ratio of the second
order to first order terms. Comparing equations (
3
) and (
4
) this ratio is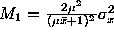
The second measure,
, is obtained from the Lagrange remainder of the Taylor series [
14
]. This provides an upper bound on the error if the series is truncated
to first order instead of using the complete expansion.
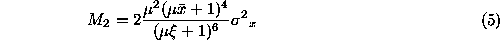
where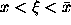
or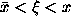
, and we compute the worst case of
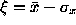for this bound in the range
.
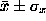is then the ratio of this truncation error to the first order term.
The significance of these measures is that they depend only on the
homography matrix elements. Thus, once a matrix has been estimated the
need for a second order approximation can be immediately assessed. In
typical imaging situations second order terms are not required. For
example, if
f
=8.5
mm
,
d
=5
m
,
t
=1
m
,
x
=50
pixels
,
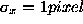, and
w
varies from
to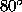
(see figure
1
b) then
| w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
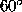
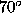
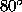
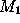
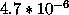
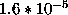
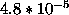
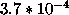
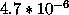
If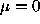
in equation (
4
) then the second order correction is zero. With
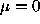the homography reduces to an affine transformation. This illustrates the
general result that if the homography is affine the first order analysis
is exact.
Generally, the
H
matrix can be decomposed into the product of matrices representing
linear
(affine) and
non linear
transformations on inhomogeneous coordinates as:
H
=
A P
where
If H is purely an affinity (linear on inhomogeneous coordinates) then P is the identity and the first order theory exact.
Antonio Criminisi