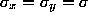 , and for the world ones
, and for the world ones . It is not strictly necessary to have such idealised distributions but
this has not been found to be a restriction in practice.
. It is not strictly necessary to have such idealised distributions but
this has not been found to be a restriction in practice.


In this section we compute the covariance of the homography
H
estimated from
n
image-world point correspondences. We consider all the computation
points to be measured with error modelled as an homogeneous, isotropic
Gaussian noise process. For the image computation points we define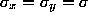 , and for the world ones
, and for the world ones . It is not strictly necessary to have such idealised distributions but
this has not been found to be a restriction in practice.
. It is not strictly necessary to have such idealised distributions but
this has not been found to be a restriction in practice.
From section
3.1
we seek the eigenvector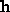 with smallest eigenvalue
with smallest eigenvalue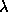 of
of . If the measured points are noise-free, or
n
= 4, then
. If the measured points are noise-free, or
n
= 4, then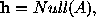 and in general we can assume that for
and in general we can assume that for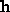 the residual error
the residual error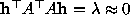 .
.
We now use matrix perturbation theory [
7
] to compute the covariance of
of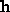 based on this zero approximation. In a similar manner to [
16
], it can be shown that the
based on this zero approximation. In a similar manner to [
16
], it can be shown that the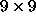 covariance matrix
covariance matrix is
is

where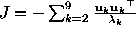 , with
, with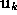 the
the eigenvector of the
eigenvector of the matrix and
matrix and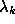 the corresponding eigenvalue.
S
is the
the corresponding eigenvalue.
S
is the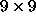 matrix:
matrix:
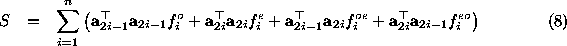
with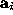
 row vector of the
A
matrix and
row vector of the
A
matrix and
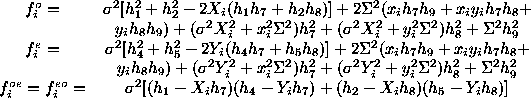
The above theory has a double advantage over other methods such as [
2
,
] which require the inverse of in order to compute
in order to compute . These methods are poorly conditioned if only four correspondences are
used, or if
n
> 4 and the correspondences are (almost) noise-free. In both cases
. These methods are poorly conditioned if only four correspondences are
used, or if
n
> 4 and the correspondences are (almost) noise-free. In both cases matrix is singular and thus is not invertible. Because the derivation of
expression (
7
) has not involved the inverse, it is well conditioned in both these
cases.
matrix is singular and thus is not invertible. Because the derivation of
expression (
7
) has not involved the inverse, it is well conditioned in both these
cases.



Antonio Criminisi