The Theil-Sen method described above estimates each parameter by the
median of the set of hypothesised parameters produced from the minimum
subsets. While this is adequate if the ellipses are described by their
conic coefficients, there is a problem when the ellipses' intrinsic
parameters are used.
Since the ellipse orientation is directional data then the median will
produce incorrect estimates if the data is clustered around the ends of
the range
.
The natural solution would be to use the circular median in place of the
linear median [
9
,
18
]. This is defined as the point
P
such that half of the data points lie on either side of the diameter
PQ
of the unit circle (on which the data lies), and that the majority of
points are closer to
P
than
Q
. However, unless the values are binned (which is undesirable since the
results will then depend on an arbitrary bin size) all pairs of points
need to be considered, which is computationally expensive. Instead, as a
compromise between efficiency and robustness, we use a combination of
the circular mean and the circular median [
9
]. We rotate the data in order to centre its circular mean at the
orientation midrange,
, a linear median is then performed, after which the rotation is undone.
Since the median can be found in linear time, calculating the
approximate circular median is also
O
(
n
).
Although the Theil-Sen estimator is more robust than the LS method, for
five dimensions its breakdown point
is only 12.9% since the fraction of outliers
must satisfy
, so that
. Although the results published in Rosin [
11
] appear to show better robustness this is possibly due to many of the
conics passing through the five-tuples being non-ellipses (i.e.
hyperbolae or parabolae) and are therefore rejected.
More robust estimators than the Theil-Sen are available, For instance, the repeated median (RM) [ 17 ] has a breakdown point of 50%, which is achieved by calculating
where
is the
q
th parameter estimated from the five points
. For
n
points this recursive application of the median results in
tuples being considered rather than the
tuples used by the Theil-Sen estimator, and is therefore two orders of
magnitude more costly in computation time. In any case, since both
and
are
, in practise evaluating all the tuples is too costly, and fitting must
be speeded up by only selecting a subset of the possible tuples. More
details on the selection of these tuples as will be described later,
however, they are not easily applicable to the repeated median
estimator.
Another robust estimator with a breakdown point of 50% is the Least
Median of Squares (LMedS) estimator [
16
], which was applied to ellipse fitting by Roth and Levine [
14
]. For each of the minimal subsets
s
they calculated the errors
from each point
to the ellipse defined by
. The LMedS ellipse has the parameters defined by the subset with the
least median error, namely
Unlike the Theil-Sen and RM estimators this application of the LMedS uses the residuals of the full data set of each hypothesised ellipse. The ideal error measure would be the Euclidean distance between the point and the ellipse, but that is expensive to calculate, requiring solving a quartic equation and choosing the smallest of the four solutions. In practice there are many simpler approximations that are often used [ 12 , 13 ]. The principle one (and both the simplest and most efficient) is the algebraic distance.
Although the LMedS method is significantly more robust than the Least Squares (LS) method it is less efficient as a statistical estimator (i.e. its asymptotic relative efficiency) as well as being generally less efficient computationally. This can be improved by ``polishing'' the fit returned by the best minimal subset. First the noise is robustly estimated using the median absolute deviation (mad) which finds the median of the errors and returns the median of the differences of the errors from that median
The median is modified by f which is a Gaussian normalisation and finite-sample correction factor [ 16 ]
and can then enable outliers to be robustly detected by applying the following indicator function
The ellipse parameters are now reestimated by performing a standard LS
fit, weighting the data points
by
to eliminate the effect of (robustly detected) outliers.
In addition to its robustness, a significant advantage of the LMedS approach just described is that all the parameters are estimated simultaneously. A weakness of the Theil-Sen and RM approaches is that each parameter is estimated independently, thereby ignoring any potential correlations between them.
We also note that the LMedS could be applied directly to the parameters rather than the residuals in a manner akin to the Theil-Sen estimator
A different approach to estimating the five ellipse parameters
simultaneously is to map the 5D parameter space onto 1D. This allows a
simple 1D estimation technique to be employed as before after which the
result is mapped [
2
] back to the full 5D parameter space. We use the Hilbert curve which
has the property that points close in 2D usually map into points close
in 1D along the curve. Since the ellipse orientation is circular it is
treated separately using the circular median. Therefore, in practice we
analyse the remaining parameters using a 4D Hilbert curve quantised so
that each axis is divided into 256 bins. The four parameters are all
measured in the same units (pixels) obviating scaling problems. Since
the Hilbert curve only covers a subset of
we must specify the desired range of each axis. In our experiments we
have set all of them to be [0,1000].
Another way to estimate the parameters simultaneously rather than performing independent 1D medians is to use a multivariate generalisation of the median. Since this is computationally expensive we use instead another robust technique: the minimum volume ellipsoid estimator (MVE) [ 16 ]. The MVE is defined as the ellipsoid with the smallest volume that contains half of the data points. It is affine invariant and so it can be easily applied to multivariate data without need for normalising the dimensions, although that is not an issue here. The centre of the MVE is used as an estimate of the ellipse parameters. As usual, the ellipse orientation is estimated separately by an approximate circular median.
To speed up calculation of the MVE it is approximated by a random resampling algorithm similar to the minimal subset method we are using for ellipse fitting. From the best estimate, robust distances are calculated for each point relative to the MVE, and are used to compute a reweighted mean [ 16 ].
All the estimators described in this paper use the minimal subsets
generated from the different combinations of data points. For the line
fitting application in [
8
] it was acceptable to use all the possible pairs of points as the
complexity was only
. Since ellipse fitting requires five-tuples taking all the combinations
would result in
complexity. Unless only very small data sets are used this in not
practically useful. However, reasonable results can still be obtained
for must less computational cost if only some of the minimal subsets are
computed. The simplest approach is just to randomly sample the data set
with replacement to generate the number of minimal subsets which is
estimated as necessary to achieve the desired likelihood of successful
performance. For instance, for the LMedS just one minimal subset
containing no outliers is sufficient for its success. This implies that
if the proportion of outliers is
, then the number of subsets
N
that must be chosen to include with
confidence one composed entirely of inliers is [
14
,
16
]
Unfortunately, this analysis only considers type II noise - the outliers. But type I noise - consisting of low level noise often modelled by additive Gaussian noise - can also have considerable effect. In our earlier work on ellipse fitting [ 11 ] it was noted that even for near perfect test cases made up from uncorrupted synthetic data many of the minimal subsets generated ellipses providing poor estimates of the full data set. Just the effects of quantising the data to the pixel grid was sufficient to substantially distort these local ellipses, particularly if the points in the minimal subset were close together. Closely spaced points have a high ``leverage'', and therefore small variations in their position have a large effect on the ellipse through the minimal subset.
Figure 1:
Orientation error of line
Figure 2:
Orientation error as a function of distance between points
The instability of the ellipse fit when points are closely spaced can
more easily be demonstrated by the example of the straight line passing
through two points. If the error of the points is bounded by
e
and the distance between the points is
d
then from figure
1
the maximum orientation error can be seen to be approximately
Plotting the error as a function of the distance between the two points
(figure
2
) shows that the error increases exponentially as the distance
decreases.
Based on work carried out to analyse the distribution of spaces on lottery tickets we can calculate the probability of smallest spacing S of r sequentially ordered items selected from n as [ 7 ]
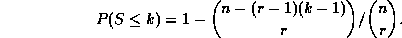
Applying this to minimal subsets for ellipses figure 3 a shows the probability of choosing five points. Naturally, as we increase the number of potential points that the subset is being drawn from the probability of two points in the subset being adjacent decreases. Nevertheless, it may appear surprising that even with 33 points there is still a 50% chance of a minimum subset of five points containing two directly adjacent members. Thus, random sampling will produce a number of subsets with closely spaced elements which could reduce their effectiveness, and therefore reduce the robustness of the estimator.
Let us take as an extreme example the situation in which minimal subsets
containing adjacent points always produce erroneous ellipses. Then for a
set of 33 points half the sampled tuples are likely to contain adjacent
points so that even an estimator with a 50% breakdown point will be
expected to have zero resistance to outliers. In general, an estimator
with a breakdown point
b
will have its effective breakdown point reduced such that the fraction
of outliers
must satisfy
This is illustrated in figure
3
b for an estimator with an original breakdown point of 0.5. Although in
practise the effects of closely spaced points will not be as extreme as
modelled here, they will have a definite lesser effect, depending on the
spatial distance between the points as well as the amount of
mislocalisation of the points.
Figure 3:
(a) Probability of choosing five points from
n
and getting a minimum spacing of one; (b) Reduced breakdown point of
estimator
Figure 4:
(a) Probability of choosing five points from
n
and getting a overall range
; (b) Probability of range being larger than a fraction
f
of the number of points
Not only are closely spaced points a problem, but points spaced too far apart can also lead to difficulties. In computer vision the data set for fitting the ellipse to is likely to be structured. For instance, the points may be sampled from a curve obtained by detecting edges in the image. This means that the outliers will not be randomly distributed among the data set. Instead, if the curve is poorly segmented then one end of the curve may be derived from the elliptical feature of interest, while the other end arises from a separate outlying object such as background clutter. When outliers are clustered like this it is better to prevent the range of the minimal subsets being too large. Otherwise, at least one point will lie on the outlying section of the curve.
If the points
in a minimal subset are randomly selected then we can analyse the joint
distribution of the spacings
between them [
7
]
Thus, the distribution of that total range that the subset covers, i.e.
, is
and is plotted for various values of
K
in figure
4
a. The likelihood of a minimal subset covering fixed a range increases
as the number of available points increases. Of more interest is when
the range of the minimal subset is taken as a fraction
f
of the full data set
n
. Replacing
K
by
gives the graph in figure
4
b. The jagged outline is due to the non-linear
operation, necessary since there is only a discrete number of points. We
can see from the graph that for small numbers of points there is a
moderate probability that a large fraction will be covered by a randomly
selected minimal subset. For example 19% of five-tuples taken from 20
points will extend to cover at least half the range of the data.
Paul L Rosin