3 Experimental Results

   
Figure 5: Examples of test data; (a) Ellipse with superimposed sine wave and Gaussian noise ( ) (b) Ellipse with superimposed sine wave and Gaussian noise ( ) (c) Ellipse with added clutter (20%) and Gaussian noise ( )

The different ellipse fitting methods were tested on synthetic data to assess their performance. Four sets of test data were used, all based on 38 points sampled from an elliptic arc (axis lengths 333 and 250, subtended angle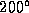 ) corrupted by Gaussian noise in the direction of the normals:

1. a sine wave was superimposed on the arc, generating some confusing small scale structure,
2. some points were additionally corrupted by extremely large amounts of Gaussian noise, producing outliers,
3. clutter was introduced (similar to structured outliers) by adding points along two noisy line segments, and
4. different lengths of the noisy arc are sampled (fewer points are taken from shorter lengths).

All the ellipse fitting methods were applied to the data, and the plots of the alpha-trimmed means of the error in the estimated ellipse centres are displayed in figure  6 . The mean is trimmed since some incorrect ellipse fits produce extremely deviant parameter estimates that have a large influence on the mean. Some of the methods occasionally failed to fit an ellipse (fitting a hyperbola or parabola instead). In these cases the fit was ignored during the calculation of the mean. The Theil-Sen method is labelled as median and LMedS params , while the LMedS method applied to the residuals is labelled as LMedS residuals 1, 2 , and 3 corresponding to the algebraic, weighted algebraic, and foci bisector distance approximations respectively. In figure  6 a, despite the presence of the superimposed sine wave, the LS method outperforms all the other methods. However, this is explained by the fact that the noise is symmetric and uniformly distributed over all the data. We can also see that the LMedS method applied to the residuals gives better results than the remaining techniques.

Figure  6 b shows how adding outliers ( and 500 for types I and II noise) causes the LS method to break down. The LMedS residual methods work best now, particularly the weighted gradient and foci bisector distance approximations which consistently produce good results so long as there is a majority of inliers. The Theil-Sen, Hilbert curve, and MVE methods produce less accurate results, and also break down earlier. However, we note that these experiments show the Theil-Sen technique breaking down later than predicted.

The addition of clutter (figure  6 c) also makes the LS estimator perform poorly, while the same two LMedS residual methods perform well again, only breaking down drastically when more than 50% of the data is made up of the clutter

We also analyse the effect of changing the angle of the arc drawn from the ellipse. The ellipse superimposed with the sinusoid was used, and the results are shown in figure  6 d. As expected reducing the angle of arc increases the error. The spike in the graph for the LS fit for arcs was surprising, but was confirmed by testing an additional 1000 random samples with a finer sampling of the angles. Many elongated ellipses tended to be fit, which may be an effect of the sinusoid.

   
Figure 6: Alpha trimmed mean error of estimated centre location ( =0.1); (a) Superimposed sine wave and Gaussian noise (b) Types I and II noise (c) Clutter and Gaussian noise (d) Reducing arclength of ellipse