


Next:
2 Improved Ellipse Fitting
Up:
Further Five Point Fit
Previous:
Further Five Point Fit
Ellipses commonly occur in man-made scenes, often being formed as the
projection of circular objects onto the image plane. They provide a
useful representation of parts of the image since 1/ they are more
convenient to manipulate than the corresponding sequences of straight
lines needed to represent the curve, and 2/ their detection is
reasonably simple and reliable. Thus they are often used by computer
vision systems for model matching [
3
,
5
]. Over the years much attention has been paid to fitting ellipses to
data samples, and many variations of the standard method for finding the
least squares (LS) solution exist [
4
,
6
]. However, computer vision often requires more robust methods that can
tolerate large amounts of outliers since there is the likelihood that
the data will be substantially corrupted by faulty feature extraction,
segmentation errors, etc. While LS is optimal under Gaussian noise it is
very sensitive to severe non-Gaussian outliers, and is therefore
unsuitable for many vision applications.
Previously we described a robust method for fitting ellipses to curve
data [
11
]. It uses the method of minimal subsets to accumulate ellipse
hypotheses. A minimal subset is the smallest number of points necessary
to uniquely define a geometric primitive (five for an ellipse). Many
five-tuples of points are selected from the full data set. Those that
define non-elliptic conics are rejected, and the remainder are
considered as hypotheses of the ellipse that best fits all the data.
Each of the intrinsic parameters of the ellipse (i.e. centre
co-ordinates, major and minor axes, and orientation) is estimated as the
median of the parameters of the hypothesised ellipses. In other words,
if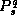 is the
q
th parameter estimated from minimal subset
s
, then the final estimates are
is the
q
th parameter estimated from minimal subset
s
, then the final estimates are for
for . This is in fact an application of the Theil-Sen estimator [
19
], which as already been used for fitting lines [
8
] and circular arcs [
10
]. Other applications of the minimal subset method to estimating
geometric features are given in references [
1
,
15
].
. This is in fact an application of the Theil-Sen estimator [
19
], which as already been used for fitting lines [
8
] and circular arcs [
10
]. Other applications of the minimal subset method to estimating
geometric features are given in references [
1
,
15
].
Unfortunately there are a number of inadequacies with the method just
described, involving 1/ the treatment of circular parameters (i.e.
orientation), 2/ statistical efficiency, and 3/ correlation between the
five parameters. This paper presents several solutions to these problems
and describes some variations on the theme of robust ellipse fitting.



Next:
2 Improved Ellipse Fitting
Up:
Further Five Point Fit
Previous:
Further Five Point Fit
Paul L Rosin
Fri Jun 20 15:05:52 BST 1997
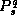 is the
q
th parameter estimated from minimal subset
s
, then the final estimates are
is the
q
th parameter estimated from minimal subset
s
, then the final estimates are for
for . This is in fact an application of the Theil-Sen estimator [
19
], which as already been used for fitting lines [
8
] and circular arcs [
10
]. Other applications of the minimal subset method to estimating
geometric features are given in references [
1
,
15
].
. This is in fact an application of the Theil-Sen estimator [
19
], which as already been used for fitting lines [
8
] and circular arcs [
10
]. Other applications of the minimal subset method to estimating
geometric features are given in references [
1
,
15
].

