


Next:
4 Experiments
Up:
Neural network experiences between
Previous:
2 Neural Network Properties
One of the most important lessons that can be extracted from the neural
network invasion that entered the pattern recognition area is that it
appears to be possible to train large, complex machines that often have
more degrees of freedom than the size of the training set. The widely
accepted dogma, based on the work by Cover, that one should never do
this has therefore to be reconsidered.
A simplified version of the traditional argumentation is that a linear
classifier in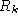 , having
k
degrees of freedom, is always able to separate perfectly an arbitrarily
labeled training set of
, having
k
degrees of freedom, is always able to separate perfectly an arbitrarily
labeled training set of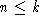 training samples and has thereby no generalization capability.
Computations by Cover [8] and later by Vapnik [4] show that
training samples and has thereby no generalization capability.
Computations by Cover [8] and later by Vapnik [4] show that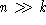 , e.g.
n
= 10
k
, in order to get some generalization. In these studies it is not taken
into account that in many applications it is known on apriori grounds
that the classes are reasonably well separable. On the same arguments as
given for the linear classifier, the more complex and nonlinear neural
network classifier should not be used in small sample size situations,
but appeared to give good results in practice.
, e.g.
n
= 10
k
, in order to get some generalization. In these studies it is not taken
into account that in many applications it is known on apriori grounds
that the classes are reasonably well separable. On the same arguments as
given for the linear classifier, the more complex and nonlinear neural
network classifier should not be used in small sample size situations,
but appeared to give good results in practice.
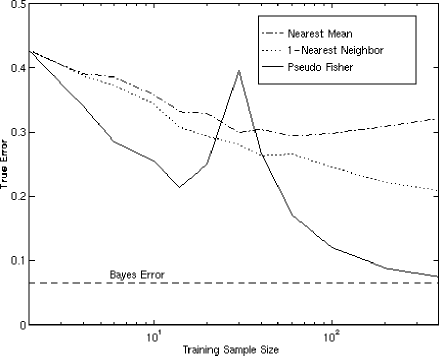
Figure 6:
The averaged error (50 runs) of some classifiers for a 30-dimensional
Gaussian problem
Stimulated by these observations the first author started to
reinvestigate the linear classifier for
n
<
k
. One of the first things that could be observed is that an adaptation
of the traditional Fisher's Linear Discriminant using a pseudo-inverse
technique (the PFLD) yields a surprising result for the separation of
two 30-dimensional Gaussian distributions [10], see fig
6
. The mean error peaks for
n
=
k
= 30. On the left side of this peak it pays off to throw away a part of
the training set at random. If this data set reduction is done more
systematically using some heuristic strategy (the Small Sample Size
Classifier, SSSC, [10]) an even better result can be obtained. This
behavior can be understood by realizing that for
n
<
k
the data is situated in a linear subspace, such that there is a
preference for directions with large variances. If these directions
coincide with the class differences, the additions of more samples, and
thereby more feature directions will mainly introduce more noise and
will yield
It should be noted that in the step from PFLD to SSSC a shift in
criterion has been made. Fisher's discriminant is based on a MSE
criterion. In case of the PFLD this criterion is still used but yields a
zero MSE as the number of parameters (the feature size) is larger than
the sample size. The SSSC now heuristically minimizes the number of
objects in the training set under the condition that still a zero MSE is
obtained. So this follows a minimum description length (MDL) strategy.
More systematically this is done by a recent proposal by Vapnik [5], the
Support Vector Classifier (SVC). If the training set is given by a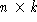 matrix
X
the weight vector
w
for a linear classifier
C
(
y
) for a new object vector
y
can be written as a linear combination of the original training set:
matrix
X
the weight vector
w
for a linear classifier
C
(
y
) for a new object vector
y
can be written as a linear combination of the original training set:
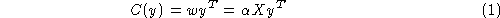
The MSE solution of a for a given set of class labels (output targets)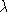 is:
is:
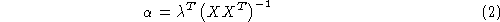
so
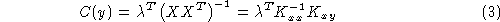
in which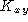 stands for the matrix of inner products between
X
and
Y
(or
y
). The FLD and the PFLD can be written like this. If
n
<=
k
the MSE is zero. In the SVC the training set X is reduced to a minimal
set. Vapnik [5] uses a quadratic programming technique which allows also
nonzero MSE solutions and thereby training set sizes
n
>
k
. He also shows that by replacing
K
by
stands for the matrix of inner products between
X
and
Y
(or
y
). The FLD and the PFLD can be written like this. If
n
<=
k
the MSE is zero. In the SVC the training set X is reduced to a minimal
set. Vapnik [5] uses a quadratic programming technique which allows also
nonzero MSE solutions and thereby training set sizes
n
>
k
. He also shows that by replacing
K
by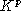 a polynomial classifier is obtained having the same complexity as the
linear one! This is due to the fact that the length of the parameter
vector a equals to size of the support set.
a polynomial classifier is obtained having the same complexity as the
linear one! This is due to the fact that the length of the parameter
vector a equals to size of the support set.
In [12] and [13] we proposed to replace the inner product matrix by an
arbitrary similarity matrix based on direct measurements of object
(dis)similarities, resulting in a featureless approach to pattern
recognition. This procedure seems to be a good candidate to meet the
challenge presented in the first section: higher image resolutions now
result in more accurate computations (of object similarities) only. The
classifier itself doesn't change. As a result of the fixed parameter
size there are no problems with an increasing complexity.

Figure 7:
Neural network error behavior as a function of the total weight size
At this point in our discussion we report an interesting perceptron
study recently undertaken by Raudys [15]. His aim is to get a better
understanding of the neural network learning behavior. In [9] we
summarized this using fig
7
. Due to the small weight initialization a neural network starts as a
linear system, for growing weights the nonlinear part of the sigmoid
function is used, see fig
3
, and for very large weights the sigmoid behaves as a threshold function
that just counts the errors. Some of Raudys' observations will now be
summarized and commented.
In order to study the linear initialization better, targets of 0.4 and
0.6 are used. Raudys proves formally and experimentally that by this the
perceptron has a MSE behavior and approaches Fisher's Linear
Discriminant. If the targets are released to extreme values, e.g. 0.001
and 0.999 the outputs are allowed to use the nonlinear part of the
sigmoid. As a result a minimum error probability behavior is found for
just weakly overlapping classes: the perceptron approaches the linear
classifier that minimizes the apparent error.
If training is proceeded further the perceptron becomes insensitive for
the most remote objects and training becomes determined by the most
nearby objects only. We suggest that if at this point the weights of the
most remote objects are set to zero, the perceptron might be used to
find a support vector classifier. So now we have a MDL solution. In the
next section an experimental examples is given. Raudys concludes that
the target value is a very important regularization parameter, in
combination with the training time. It has to be studied further how
Raudys' results should be extended to the nonlinear case for neural
networks with more layers.
A remarkable conclusion can be drawn from Raudys' study. A neural
network is not just able to implement almost any classification
function, but it can also be trained with various strategies. We add to
this conclusion that this neural network ability may only be judged
positively if it appears to be possible to formulate explicit rules how
this has to be done for an arbitrary problem. Otherwise this neural
network ability remains hidden in the skills of the analyst.



Next:
4 Experiments
Up:
Neural network experiences between
Previous:
2 Neural Network Properties
Adrian F Clark
Thu Jul 24 13:42:08 BST 1997
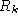 , having
k
degrees of freedom, is always able to separate perfectly an arbitrarily
labeled training set of
, having
k
degrees of freedom, is always able to separate perfectly an arbitrarily
labeled training set of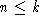 training samples and has thereby no generalization capability.
Computations by Cover [8] and later by Vapnik [4] show that
training samples and has thereby no generalization capability.
Computations by Cover [8] and later by Vapnik [4] show that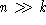 , e.g.
n
= 10
k
, in order to get some generalization. In these studies it is not taken
into account that in many applications it is known on apriori grounds
that the classes are reasonably well separable. On the same arguments as
given for the linear classifier, the more complex and nonlinear neural
network classifier should not be used in small sample size situations,
but appeared to give good results in practice.
, e.g.
n
= 10
k
, in order to get some generalization. In these studies it is not taken
into account that in many applications it is known on apriori grounds
that the classes are reasonably well separable. On the same arguments as
given for the linear classifier, the more complex and nonlinear neural
network classifier should not be used in small sample size situations,
but appeared to give good results in practice.



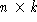 matrix
X
the weight vector
w
for a linear classifier
C
(
y
) for a new object vector
y
can be written as a linear combination of the original training set:
matrix
X
the weight vector
w
for a linear classifier
C
(
y
) for a new object vector
y
can be written as a linear combination of the original training set: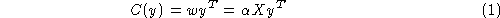
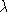 is:
is: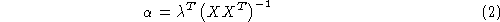
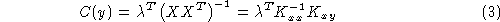
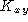 stands for the matrix of inner products between
X
and
Y
(or
y
). The FLD and the PFLD can be written like this. If
n
<=
k
the MSE is zero. In the SVC the training set X is reduced to a minimal
set. Vapnik [5] uses a quadratic programming technique which allows also
nonzero MSE solutions and thereby training set sizes
n
>
k
. He also shows that by replacing
K
by
stands for the matrix of inner products between
X
and
Y
(or
y
). The FLD and the PFLD can be written like this. If
n
<=
k
the MSE is zero. In the SVC the training set X is reduced to a minimal
set. Vapnik [5] uses a quadratic programming technique which allows also
nonzero MSE solutions and thereby training set sizes
n
>
k
. He also shows that by replacing
K
by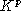 a polynomial classifier is obtained having the same complexity as the
linear one! This is due to the fact that the length of the parameter
vector a equals to size of the support set.
a polynomial classifier is obtained having the same complexity as the
linear one! This is due to the fact that the length of the parameter
vector a equals to size of the support set.