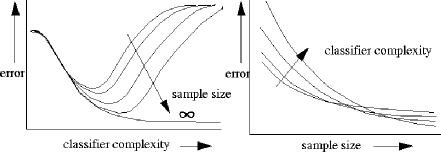
Figure 1: The behavior of the classification error as a function of the classifier complexity (e.g. feature size or number of degrees of freedom) and the size of the training set



The purpose of this paper is to sketch the neural network contribution to the pattern recognition area. We will concentrate on feed-forward networks and pattern classifiers. As this is not review paper the references will be mainly restricted to a few general books and papers ([1]-[7]) that might be useful for further reading and to some contributions by the authors and others that support the private observations and evaluations of the discussed approaches.
The challenge for the pattern recognition researcher can be simply formulated as: define an automatic procedure that, given a collection of sets of different real world objects is able to find the correct set for a new object. These sets are usually called classes and their names labels. The procedure is a pattern classifier as it has to find the patterns distinguishing the classes from the given collection of examples, often referred to as the training set: a collection of object with known labels. Examples of such pattern recognition problems are the recognition of apples and pears, gothic and roman churches, or more applicable, handwritten characters, spoken words and microscopically observed biological tissues and cells. Human beings are reasonably able to learn to recognize these types of objects using relatively small sets of examples: tens to hundreds. How about an automatic procedure?
It has been realized for a long time that a single, generally applicable pattern recognition system cannot work without any context information. For that reason the abstraction has been made to represent objects by features: measurements from which an expert in the application knows that they are useful for finding the patterns. The training set is herewith reduced to a set of labeled points in a feature vector space and the pattern classifier to a discriminant function defining or separating areas for different classes in this space.
There is a major problem with this approach: for some application areas no expert can be found able to define a small set of good features. For instance, for the character recognition problem many feature types have been proposed, cumulating in thousands of different features. As a direct consequence the question has to be faced: how does the size of the feature space (its dimensionality) affect the generalization (performance) of a pattern classifier? If also the possibility of patterns defined by nonlinear combinations of features has to be included, the question can be reformulated as: How are the complexity and the generalization capability of a classifier related?
This question cannot be answered without considering the size of the training set as well. If we have an infinitely large set of examples the most complex classifier will describe the pattern better or equally good as more simple systems. For finite sample sizes, however, very complex classifiers may also be able to find very detailed patterns, in fact caused by the noise. These classifiers will have a bad performance. As a consequence, more simple classifiers might perform better than more complex classifiers in case of finite sample size, see fig 1 . This phenomenon is known under various names in the pattern recognition literature: peaking, the curse of dimensionality, Rao's paradox and Hughes' phenomenon.

Figure 1:
The behavior of the classification error as a function of the classifier
complexity (e.g. feature size or number of degrees of freedom) and the
size of the training set
For a given classifier a peaking performance can only be avoided by a sufficiently large sample size. For difficult classification problems (those that need complex classifiers) it appears sometimes to be necessary to have hundreds of thousands of training objects. More complex classifiers are caused, among others, by growing feature sizes. It remains counterintuitive that better object descriptions, e.g. more pixels caused by higher resolution images, may result in a worse performance and thereby demand more object examples, see fig 2 . We will return to this point at the end of the paper.

Figure 2:
Higher resolutions may result in more features and thereby in a worse
performance
The classifier complexity still lacks a useful definition. For classifiers that are linear in their parameters it can be defined as the number of degrees of freedom. Vapnik [4] has given a definition for nonlinear classifiers as well, which is, however, related to a worst case training set of unknown probability. Moreover, the above curves are problem dependent. So what is really needed for an optimal classifier choice is some method that connects the classifier complexity with the difficulty of the problem: the data complexity. This is still an open issue.
This approach of estimating first the desired complexity (which includes the choice of feature set) finally aims at an automatic procedure that chooses for a given problem the best classifier (in some sense) and thereby constitutes a `super classifier', which has to be used for all pattern classification problems. Herewith the question is raised why we cannot build directly a classifier that automatically adapts itself to the optimal complexity.
This point of view makes it necessary to reconsider the traditional optimization criteria for classifiers. The two most frequently used are the error probability and the mean square error . The first is based on some integration of the classification error and is directly related to what is considered as the performance of the final classifier. The second is based on distance measures, which are usually easier to calculate and to optimize but which are only indirectly related to the classifier performance. Both measures, however, do not include any complexity measure. Thereby they are not protected against peaking during the optimization of a classifier with an adjustable complexity. A possibly third approach is the minimization of the description length , which seems directly related to the complexity. For a straight forward use of this approach it is necessary to fix the classification error.
In any discussion on comparing and selecting classifiers it is necessary to realize that the overall performance of a classifier depends on the set of problems that is considered. No classifier will be the best on any problem or on any set of problems. So it is necessary to make a choice on a wide set of problems. See [2] for an example of such a study. In [11] the problem of comparing classifier is discussed more extensively.
In the remainder of this paper the feed-forward neural network classifier is discussed in the light of the above considerations. It will be summarized what can be learnt from this classifier and these insights will be applied to the extension of traditional classifiers and the development of new classifiers.



Adrian F Clark