


Next:
5 Results
Up:
A Method of
Previous:
3 Polyhedral-Based Correspondence
Given a pair of corresponding sparse polyhedra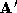 and
and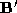 , a local surface parameterisation is used to interpolate a dense set of
vertices on each. The local surface parameterisation is of a single
sparse triangle, and is produced by a parameterisation of the three
surface paths corresponding to its three edges. If the triangles of the
two sparse polyhedra correspond, then so will the interpolated vertices
wtihin them. The connectivity of these vertices is defined by the
interpolation. The interpolated vertices of this dense corresponding
pair may then be merged by combining the geometric information from
both, with the connectivity description which is identical in each.
, a local surface parameterisation is used to interpolate a dense set of
vertices on each. The local surface parameterisation is of a single
sparse triangle, and is produced by a parameterisation of the three
surface paths corresponding to its three edges. If the triangles of the
two sparse polyhedra correspond, then so will the interpolated vertices
wtihin them. The connectivity of these vertices is defined by the
interpolation. The interpolated vertices of this dense corresponding
pair may then be merged by combining the geometric information from
both, with the connectivity description which is identical in each.
We now describe an algorithm which produces a parameterised
path
across the surface of a densely triangulated polygon between two
vertices and
and of its sparsely triangulated approximation. This surface path forms the
basis of a local parameterisation of surface patches (sparse polyhedral
triangles).
of its sparsely triangulated approximation. This surface path forms the
basis of a local parameterisation of surface patches (sparse polyhedral
triangles).
The algorithm works in a similar fashion to a distance transform
algorithm. We imagine a
fire
started at , which spreads out in all directions along connected triangle edges,
burning continuously until it reaches
, which spreads out in all directions along connected triangle edges,
burning continuously until it reaches . The rate of burn is determined by a metric
f
. Only a finite number of points are considered on the boundary of the
fire at any one time. These are the set of edges
. The rate of burn is determined by a metric
f
. Only a finite number of points are considered on the boundary of the
fire at any one time. These are the set of edges connected to the edge
connected to the edge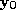 upon which the current end point
upon which the current end point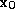 of the surface path is located, see Figure 2. Each of these connected
boundary
edges has an identified best point which is a possible new point on the
surface path. The edge
of the surface path is located, see Figure 2. Each of these connected
boundary
edges has an identified best point which is a possible new point on the
surface path. The edge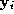 with the smallest metric value is selected to
burn
next, and the best surface path point
with the smallest metric value is selected to
burn
next, and the best surface path point upon it becomes the new end of the surface path. The new edge
upon it becomes the new end of the surface path. The new edge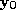 now ignites all its unburnt neighbours
now ignites all its unburnt neighbours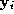 (at a certain cost
C
) and attaches to each the following function value:
(at a certain cost
C
) and attaches to each the following function value:

where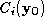 is the cost of
igniting
is the cost of
igniting
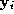 from
from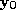 . The function
f
increases monotonically along any given surface path. The manner in
which the fire burns (i.e. always consider the edge with minimum cost so
far) guarantees that we find the minimum cost path from
. The function
f
increases monotonically along any given surface path. The manner in
which the fire burns (i.e. always consider the edge with minimum cost so
far) guarantees that we find the minimum cost path from to
to . The algorithm is made more computationally efficient by burning two
fires simultaneously from
. The algorithm is made more computationally efficient by burning two
fires simultaneously from to
to and from
and from to
to until the boundaries of the two fires intersect.
until the boundaries of the two fires intersect.

Figure 3:
Surfaces are made densely triangulated by the recursive splitting of
triangles into groups of four sub-triangles.
Figure 2:
Surface paths are defined on the dense triangulation of the surface by
the parameterisation of triangle edges.
We now describe the function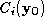 . The minimisation of this cost locates the best next point for the
surface path. A point
. The minimisation of this cost locates the best next point for the
surface path. A point on edge
on edge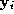 can be expressed parametrically by:
can be expressed parametrically by:

where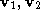 are the vertices on the mesh which define the edge
are the vertices on the mesh which define the edge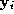 . We consider not just the path
. We consider not just the path which is a sparse polyhedral edge, but also the sparse polyhedral
triangles connected to this which have vertices
which is a sparse polyhedral edge, but also the sparse polyhedral
triangles connected to this which have vertices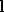 and
and , see Figure 4.
, see Figure 4.

Figure 4:
The cost function used to produce surface paths is defined in terms of a
pair of sparse polyhedral triangles connected along an edge.
We define a point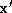 which is the projection of
which is the projection of onto the sparse edge
onto the sparse edge , again see Figure 4:
, again see Figure 4:
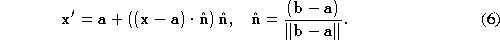
Now, we define a series of lengths:

from which the cost function of igniting an edge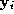 from edge
from edge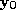 may be defined as:
may be defined as:

which may be minimised in
s
to find . The minimisation of expression
. The minimisation of expression forces the surface path over hills, to follow a `straight' line between
forces the surface path over hills, to follow a `straight' line between and
and . The minimisation of
. The minimisation of constrains the surface path to lie within the two triangles defined by
constrains the surface path to lie within the two triangles defined by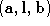 and
and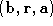 thus preventing it from looping back around the entire surface.
thus preventing it from looping back around the entire surface.
The connectivity of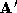 and
and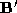 are identical. Therefore, we can correspond the individual sparse
triangles of the polyhedra. A dense set of corresponded sampling points
may then be generated within each pair of triangles. First, the three
surface paths corresponding to the edges of a sparse triangle are
extracted using the method of the previous section. Next, three new
vertices are defined at the midpoints of these paths. The triangle is
now split into four new sub-triangles, see Figure 3. This process is
applied to all the triangles of
are identical. Therefore, we can correspond the individual sparse
triangles of the polyhedra. A dense set of corresponded sampling points
may then be generated within each pair of triangles. First, the three
surface paths corresponding to the edges of a sparse triangle are
extracted using the method of the previous section. Next, three new
vertices are defined at the midpoints of these paths. The triangle is
now split into four new sub-triangles, see Figure 3. This process is
applied to all the triangles of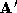 and
and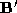 recursively to some
depth
to produce the dense triangulation
recursively to some
depth
to produce the dense triangulation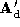 and
and .
.
Now a densely triangulated mean shape may be generated. The recursive
triangle-splitting algorithm is applied to all of the triangles of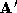 and
and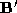 until
until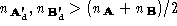 . The geometric information from these is then averaged to produce a
pointset
. The geometric information from these is then averaged to produce a
pointset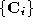 and this is combined with the connectivity from either
and this is combined with the connectivity from either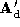 or
or to produce a densely triangulated polyhedron
to produce a densely triangulated polyhedron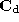 . Finally,
. Finally,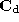 is decimated to the required average number of vertices
is decimated to the required average number of vertices to produce our densely triangulated mean
to produce our densely triangulated mean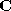 , see Figure 5.
, see Figure 5.
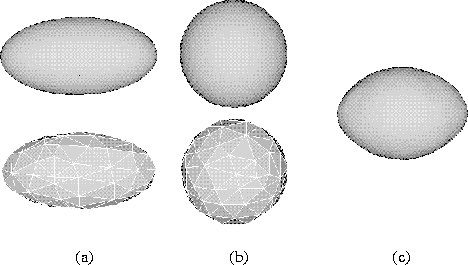
Figure 5:
The mean of two synthetic shapes. (a) and (b) are a pair of triangulated
surfaces defining an ellipsoid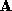 and a sphere
and a sphere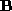 . The upper surfaces are the original dense triangulation of
approximately 800 vertices. The lower surfaces are the polyhedral
approximations to these used for correspondence by the ICP algorithm,
. The upper surfaces are the original dense triangulation of
approximately 800 vertices. The lower surfaces are the polyhedral
approximations to these used for correspondence by the ICP algorithm,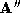 and
and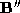 . The approximations have been decimated by 90%. (c) is the dense
triangulated mean shape
. The approximations have been decimated by 90%. (c) is the dense
triangulated mean shape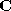 of these two examples.
of these two examples.



Next:
5 Results
Up:
A Method of
Previous:
3 Polyhedral-Based Correspondence
Alan Brett
Wed Jul 9 16:24:02 BST 1997
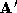 and
and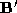 , a local surface parameterisation is used to interpolate a dense set of
vertices on each. The local surface parameterisation is of a single
sparse triangle, and is produced by a parameterisation of the three
surface paths corresponding to its three edges. If the triangles of the
two sparse polyhedra correspond, then so will the interpolated vertices
wtihin them. The connectivity of these vertices is defined by the
interpolation. The interpolated vertices of this dense corresponding
pair may then be merged by combining the geometric information from
both, with the connectivity description which is identical in each.
, a local surface parameterisation is used to interpolate a dense set of
vertices on each. The local surface parameterisation is of a single
sparse triangle, and is produced by a parameterisation of the three
surface paths corresponding to its three edges. If the triangles of the
two sparse polyhedra correspond, then so will the interpolated vertices
wtihin them. The connectivity of these vertices is defined by the
interpolation. The interpolated vertices of this dense corresponding
pair may then be merged by combining the geometric information from
both, with the connectivity description which is identical in each.


 and
and of its sparsely triangulated approximation. This surface path forms the
basis of a local parameterisation of surface patches (sparse polyhedral
triangles).
of its sparsely triangulated approximation. This surface path forms the
basis of a local parameterisation of surface patches (sparse polyhedral
triangles). connected to the edge
connected to the edge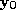 upon which the current end point
upon which the current end point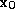 of the surface path is located, see Figure 2. Each of these connected
boundary
edges has an identified best point which is a possible new point on the
surface path. The edge
of the surface path is located, see Figure 2. Each of these connected
boundary
edges has an identified best point which is a possible new point on the
surface path. The edge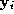 with the smallest metric value is selected to
burn
next, and the best surface path point
with the smallest metric value is selected to
burn
next, and the best surface path point upon it becomes the new end of the surface path. The new edge
upon it becomes the new end of the surface path. The new edge
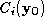 is the cost of
igniting
is the cost of
igniting

 on edge
on edge
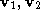 are the vertices on the mesh which define the edge
are the vertices on the mesh which define the edge which is a sparse polyhedral edge, but also the sparse polyhedral
triangles connected to this which have vertices
which is a sparse polyhedral edge, but also the sparse polyhedral
triangles connected to this which have vertices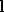 and
and , see Figure 4.
, see Figure 4.
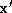 which is the projection of
which is the projection of onto the sparse edge
onto the sparse edge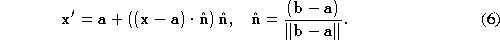


 forces the surface path over hills, to follow a `straight' line between
forces the surface path over hills, to follow a `straight' line between constrains the surface path to lie within the two triangles defined by
constrains the surface path to lie within the two triangles defined by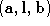 and
and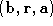 thus preventing it from looping back around the entire surface.
thus preventing it from looping back around the entire surface.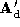 and
and .
.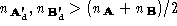 . The geometric information from these is then averaged to produce a
pointset
. The geometric information from these is then averaged to produce a
pointset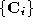 and this is combined with the connectivity from either
and this is combined with the connectivity from either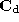 . Finally,
. Finally, to produce our densely triangulated mean
to produce our densely triangulated mean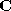 , see Figure 5.
, see Figure 5.
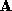 and a sphere
and a sphere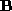 . The upper surfaces are the original dense triangulation of
approximately 800 vertices. The lower surfaces are the polyhedral
approximations to these used for correspondence by the ICP algorithm,
. The upper surfaces are the original dense triangulation of
approximately 800 vertices. The lower surfaces are the polyhedral
approximations to these used for correspondence by the ICP algorithm,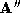 and
and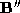 . The approximations have been decimated by 90%. (c) is the dense
triangulated mean shape
. The approximations have been decimated by 90%. (c) is the dense
triangulated mean shape