In order to test the pair-wise correspondence and merging algorithms, we have constructed a binary tree of merged shapes. The shapes are three examples of the left ventricle of the brain. These have been defined by hand as contours on a series of 2D slices from 3D Magnetic Resonance images. The ventricles of the brain have a complex structure and vary significantly between individuals in both their size and shape.
The tree of merged shapes is shown in Figure 6 as a series of shaded and rendered triangulated surfaces. The first level shows three input example shapes. The second level shows the means of the upper and lower pairs of level 1. Level 3 is the merged mean of the two shapes in level 2 and represents the mean shape of the three input examples. In each case, the original triangulated surface was decimated by 90% to produce the sparse polyhedral representation during matching.
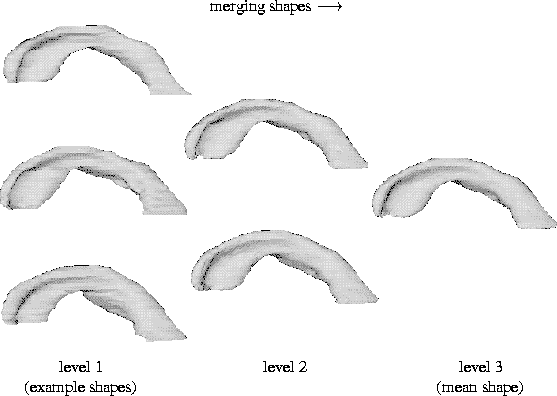
Figure 6:
A merge tree of three examples of the left ventricle of the brain. Level
1 shows the three original example shapes which are merged to produce
the two densely triangulated mean shapes of level 2. These shapes have
been merged to produce the mean shape of level 3. At each level of the
tree, the shape is a mean of the two shapes immediately above and below
it in the level to its left.
The pair-wise correspondence and merging algorithms have proved to be
computationally tractable - the matching of two ventricular surfaces (
vertices) using a decimation of 90% for the sparse polyhedral
representations takes around 70 CPU seconds on a Sun UltraSPARC 2. The
merging algorithm takes a further 90 CPU seconds to produce a densely
triangulated mean from the resulting matched sparse polyhedrons.
Alan Brett