


Next:
4 Case of Polyhedral
Up:
3 Problem Definition
Previous:
3.2 Constraint Representation
The parameter vector has to minimize the objective function (
5
) subject to the constraints (
6
) and (
7
) imposed by the model. So, the problem that we are dealing with is a
constrained optimization problem to which an optimal solution may be
provided by minimizing the following energy function:
has to minimize the objective function (
5
) subject to the constraints (
6
) and (
7
) imposed by the model. So, the problem that we are dealing with is a
constrained optimization problem to which an optimal solution may be
provided by minimizing the following energy function:
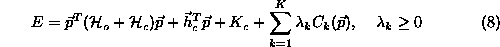
known in the literature as the Lagrangian function. the above function
contains two components, the least squares function:

and the constraint function:

The method of solving this problem depends on the nature of the
objective function (convex or not), the type of the constraints (linear
or not) and whether the constraints could be merged together in order to
reduce the number of parameters and eventually combined with the least
square objective function.
The objective function is convex since it is quadratic and the matrix is positive definite (since each matrix
is positive definite (since each matrix is positive definite). The same propriety can be satisfied by
is positive definite). The same propriety can be satisfied by as well.
as well.
So the problem can be said to be a convex optimization problem if the
constraints are also convex functions. On the other hand, the existence of an
optimal solution necessitates that both the least squares function and
the constraint function are differentiable. A detailed analysis of the
convexity and the optimality conditions is available in [
7
].
are also convex functions. On the other hand, the existence of an
optimal solution necessitates that both the least squares function and
the constraint function are differentiable. A detailed analysis of the
convexity and the optimality conditions is available in [
7
].
In some particular cases it is possible to get a closed form solution of
(
8
). This depends of the characteristics of the constraint functions and
whether it is possible to combine them efficiently with the objective
function. But generally, it is not trivial to develop a closed form
solution especially when the constraints are nonlinear and their number
is high. In such case, an algorithmic approach could be of great help
taking into account the increasing capabilities of computing. The main
idea was to develop a search optimization scheme for determining the
best set . Moreover, we have been seeing whether it is possible that one can get
the solution which satisfies a desired tolerance. So the objective is to
determine the vector
. Moreover, we have been seeing whether it is possible that one can get
the solution which satisfies a desired tolerance. So the objective is to
determine the vector which satisfies the constraints to the desired accuracy and which fits
the data to a reasonable degree.
which satisfies the constraints to the desired accuracy and which fits
the data to a reasonable degree.
To solve the optimization problem, we have simplified the full problem
slightly. As first step, we have given an equal weight to each
constraint, so a single is considered for all the constraints:
is considered for all the constraints:

The problem now is how to find that minimizes (
11
). Because (
11
) may be a non-convex problem (thus having local minima), we solve the
problem in a style similar to the GNC method [
1
]. That is we start with a parameter vector
that minimizes (
11
). Because (
11
) may be a non-convex problem (thus having local minima), we solve the
problem in a style similar to the GNC method [
1
]. That is we start with a parameter vector that satisfies the least squares constraints, and attempt to find a
nearby vector
that satisfies the least squares constraints, and attempt to find a
nearby vector that minimizes (
11
) for small
that minimizes (
11
) for small (in which the constraints are weakly expressed). Then iteratively, we
increase
(in which the constraints are weakly expressed). Then iteratively, we
increase slightly and solve for a new optimal parameter
slightly and solve for a new optimal parameter using the previous
using the previous . While we cannot (so far) guarantee that we converge to an optimal
value, at least so far we have not seen cases of suboptimal solutions.
. While we cannot (so far) guarantee that we converge to an optimal
value, at least so far we have not seen cases of suboptimal solutions.
At each iteration
n
the algorithm increases by a certain amount, and a new
by a certain amount, and a new is found such that the optimization function is minimized by means of
the standard Levenberg-Marquardt algorithm. The parameter vector
is found such that the optimization function is minimized by means of
the standard Levenberg-Marquardt algorithm. The parameter vector is then updated to the new estimate
is then updated to the new estimate which become the initial estimate at the next value of
which become the initial estimate at the next value of . The algorithm stops when the constraints are satisfied to the desired
degree, or when the parameter vector remains stable for a certain number
of iterations. The above algorithm is illustrated in Figure
1
a.
. The algorithm stops when the constraints are satisfied to the desired
degree, or when the parameter vector remains stable for a certain number
of iterations. The above algorithm is illustrated in Figure
1
a.

Figure 1:
(a):
optim1
- batch constraint optimization algorithm. (b):
optim2
- sequential constraint introduction optimization algorithm.
The initialization of the parameter vector is crucial to guarantee the
convergence of the algorithm to the desired solution. For this reason
the initial vector should be taken as the one which best fitted the set
of data. This vector can be obtained by estimating each surface's
parameter vector separately and then concatenating the vectors into a
single one. Naturally the option of minimizing the least squares
function alone has to be avoided since it leads to the trivial null vector
solution. On another hand, the initial value
alone has to be avoided since it leads to the trivial null vector
solution. On another hand, the initial value has to be large enough in order to avoid first the above trivial
solution and second to give the constraints a certain weight. A
convenient value for the initial
has to be large enough in order to avoid first the above trivial
solution and second to give the constraints a certain weight. A
convenient value for the initial is
is
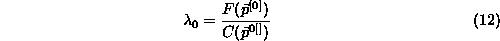
where is the initial parameter estimation.
is the initial parameter estimation.
Another option of the algorithm consists of adding the constraints
incrementally. At each step a new constraint is added to the constraint
function and then the optimal value of
and then the optimal value of is found according to the scheme shown in Figure
1
b. For each new added constraint
is found according to the scheme shown in Figure
1
b. For each new added constraint ,
, is initialized at
is initialized at , whereas
, whereas is kept at its current value.
is kept at its current value.



Next:
4 Case of Polyhedral
Up:
3 Problem Definition
Previous:
3.2 Constraint Representation
Naoufel Werghi
Thu Jul 10 17:36:04 BST 1997
 has to minimize the objective function (
5
) subject to the constraints (
6
) and (
7
) imposed by the model. So, the problem that we are dealing with is a
constrained optimization problem to which an optimal solution may be
provided by minimizing the following energy function:
has to minimize the objective function (
5
) subject to the constraints (
6
) and (
7
) imposed by the model. So, the problem that we are dealing with is a
constrained optimization problem to which an optimal solution may be
provided by minimizing the following energy function:


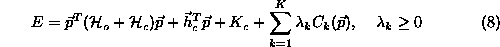


 is positive definite (since each matrix
is positive definite (since each matrix is positive definite). The same propriety can be satisfied by
is positive definite). The same propriety can be satisfied by as well.
as well. are also convex functions. On the other hand, the existence of an
optimal solution necessitates that both the least squares function and
the constraint function are differentiable. A detailed analysis of the
convexity and the optimality conditions is available in [
are also convex functions. On the other hand, the existence of an
optimal solution necessitates that both the least squares function and
the constraint function are differentiable. A detailed analysis of the
convexity and the optimality conditions is available in [ . Moreover, we have been seeing whether it is possible that one can get
the solution which satisfies a desired tolerance. So the objective is to
determine the vector
. Moreover, we have been seeing whether it is possible that one can get
the solution which satisfies a desired tolerance. So the objective is to
determine the vector which satisfies the constraints to the desired accuracy and which fits
the data to a reasonable degree.
which satisfies the constraints to the desired accuracy and which fits
the data to a reasonable degree. is considered for all the constraints:
is considered for all the constraints:
 that minimizes (
that minimizes ( that satisfies the least squares constraints, and attempt to find a
nearby vector
that satisfies the least squares constraints, and attempt to find a
nearby vector that minimizes (
that minimizes ( (in which the constraints are weakly expressed). Then iteratively, we
increase
(in which the constraints are weakly expressed). Then iteratively, we
increase slightly and solve for a new optimal parameter
slightly and solve for a new optimal parameter using the previous
using the previous . While we cannot (so far) guarantee that we converge to an optimal
value, at least so far we have not seen cases of suboptimal solutions.
. While we cannot (so far) guarantee that we converge to an optimal
value, at least so far we have not seen cases of suboptimal solutions. by a certain amount, and a new
by a certain amount, and a new is found such that the optimization function is minimized by means of
the standard Levenberg-Marquardt algorithm. The parameter vector
is found such that the optimization function is minimized by means of
the standard Levenberg-Marquardt algorithm. The parameter vector is then updated to the new estimate
is then updated to the new estimate which become the initial estimate at the next value of
which become the initial estimate at the next value of . The algorithm stops when the constraints are satisfied to the desired
degree, or when the parameter vector remains stable for a certain number
of iterations. The above algorithm is illustrated in Figure
. The algorithm stops when the constraints are satisfied to the desired
degree, or when the parameter vector remains stable for a certain number
of iterations. The above algorithm is illustrated in Figure
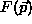 alone has to be avoided since it leads to the trivial null vector
solution. On another hand, the initial value
alone has to be avoided since it leads to the trivial null vector
solution. On another hand, the initial value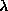 has to be large enough in order to avoid first the above trivial
solution and second to give the constraints a certain weight. A
convenient value for the initial
has to be large enough in order to avoid first the above trivial
solution and second to give the constraints a certain weight. A
convenient value for the initial is
is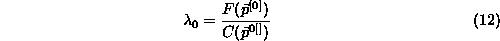
 is the initial parameter estimation.
is the initial parameter estimation. and then the optimal value of
and then the optimal value of is found according to the scheme shown in Figure
is found according to the scheme shown in Figure ,
, is initialized at
is initialized at , whereas
, whereas is kept at its current value.
is kept at its current value.