


Up:
Degenerate Models of Additive
Previous:
References
Our analysis to degenerate solutions of motion transparency are based
upon a singular value decomposition (SVD) of image measurements[
1
]. Consider the vector of measurements that are collected into an
of measurements that are collected into an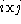 matrix
matrix . The singular value decomposition is given by
. The singular value decomposition is given by
 where the columns of
where the columns of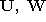 are orthonormal and
are orthonormal and is a diagonal square-root matrix. Let
is a diagonal square-root matrix. Let be the
be the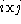 matrix of rank
matrix of rank formed from the
formed from the largest singular values, and singular vectors of
largest singular values, and singular vectors of . Then
. Then is the rank
is the rank least-squares approximation of
least-squares approximation of in that it minimises:
in that it minimises:

for all matrices of rank
of rank or less [
6
]. Accordingly, we partition
or less [
6
]. Accordingly, we partition as:
as:

The matrix of residuals and signal is:

From equation (
2
), there are three combinations of second order derivatives that yield
coherent motion. They are:

In our coherent model, we have combined the first two to permit a
least-squares estimate of image velocity from the SVD of . So that we have
n
= 6 and
. So that we have
n
= 6 and . Using the first two constraints from equation (
16
) we consider the model:
. Using the first two constraints from equation (
16
) we consider the model:

where is a residual. We now minimise this model according to:
is a residual. We now minimise this model according to:
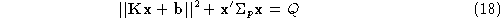
where and
Q
is again a residual after including
and
Q
is again a residual after including .
. for a single motion can be viewed as a Lagrangian based upon the phase
velocity. Also,
for a single motion can be viewed as a Lagrangian based upon the phase
velocity. Also, . From this, the model's parameters are obtained from:
. From this, the model's parameters are obtained from:

where
k
refers to the number of measurements taken and the unbiased estimate of the variance
the unbiased estimate of the variance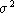 . Note, a small value of
Q
, requires that the third row and column of the matrix
. Note, a small value of
Q
, requires that the third row and column of the matrix : a null vector. This will occur when the regression matrix
: a null vector. This will occur when the regression matrix is of full rank, the variation
is of full rank, the variation is large by comparision to the variation of the measurements, and the
measured temporal derivatives are small in magnitude.
is large by comparision to the variation of the measurements, and the
measured temporal derivatives are small in magnitude.
An estimate of the generalised covariance of the measurements is given
by:

The model with the smallest generalised variance implies one whose
stability is highest. Equally, we can consider the model which takes
into account the most variance. To do this, we define the confidence
measure taken from the geometric mean of the eigenvalues to the regression
matrix
taken from the geometric mean of the eigenvalues to the regression
matrix
 :
:

where and
C
is a constant. Equation (
21
) may be regarded as a test statistic that the matrix
and
C
is a constant. Equation (
21
) may be regarded as a test statistic that the matrix has a simple form like
has a simple form like [
6
], and
[
6
], and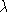 is large. We have used this measure to determine our model certainty
estimates because it reflects the stability of a model's parameters
posed in terms of the total variation of the image measurements.
is large. We have used this measure to determine our model certainty
estimates because it reflects the stability of a model's parameters
posed in terms of the total variation of the image measurements.
The 1-d (phase) velocity and the confidence measure used to obtain the curves shown in figure
3
was taken from the model:
and the confidence measure used to obtain the curves shown in figure
3
was taken from the model:

whose parameters were determined from the first eigenvector to the SVD
of the matrix [
1
].
[
1
].
Degeneracies of rank 3 or 4 to a 2-fold transparent motion model are
ambiguous (ie to cases of three or four sinusoids) and not considered
here. Feasible solutions may, however, be obtained using linear
optimisation and the constraints given by equations (6)-(8). A unique
single-flow vector may be detected if the system is determined to be of
rank 3. Here one is required to collect the three constraints from
equation (
16
) from their respective eigenvector elements of the 3 largest
eigenvalues to the matrix
A
into a single least-squares system.



Up:
Degenerate Models of Additive
Previous:
References
Adrian F Clark
Tue Jul 22 15:38:58 BST 1997
 of measurements that are collected into an
of measurements that are collected into an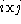 matrix
matrix . The singular value decomposition is given by
. The singular value decomposition is given by
 where the columns of
where the columns of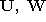 are orthonormal and
are orthonormal and is a diagonal square-root matrix. Let
is a diagonal square-root matrix. Let be the
be the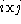 matrix of rank
matrix of rank formed from the
formed from the largest singular values, and singular vectors of
largest singular values, and singular vectors of . Then
. Then is the rank
is the rank least-squares approximation of
least-squares approximation of in that it minimises:
in that it minimises:



 of rank
of rank


 . Using the first two constraints from equation (
. Using the first two constraints from equation (
 is a residual. We now minimise this model according to:
is a residual. We now minimise this model according to: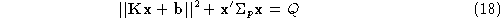
 and
Q
is again a residual after including
and
Q
is again a residual after including .
. . From this, the model's parameters are obtained from:
. From this, the model's parameters are obtained from:
 the unbiased estimate of the variance
the unbiased estimate of the variance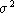 . Note, a small value of
Q
, requires that the third row and column of the matrix
. Note, a small value of
Q
, requires that the third row and column of the matrix : a null vector. This will occur when the regression matrix
: a null vector. This will occur when the regression matrix is of full rank, the variation
is of full rank, the variation
 taken from the geometric mean of the eigenvalues to the regression
matrix
taken from the geometric mean of the eigenvalues to the regression
matrix

 and
C
is a constant. Equation (
and
C
is a constant. Equation ( has a simple form like
has a simple form like [
[ is large. We have used this measure to determine our model certainty
estimates because it reflects the stability of a model's parameters
posed in terms of the total variation of the image measurements.
is large. We have used this measure to determine our model certainty
estimates because it reflects the stability of a model's parameters
posed in terms of the total variation of the image measurements. and the confidence measure used to obtain the curves shown in figure
and the confidence measure used to obtain the curves shown in figure