2 Multiplicative Transparent Models

Shizawa and Mase[ 10 ] posed derivative constraints based upon cascades of the motion constraint equation; one for each of the transparent motions. Using a phase-based approach, Langley et al.[ 9 ] forwarded a similar constraint from bandpass filters that required only one order of differentiation. The model considered here combines both. It is based on an implicit logarithmic nonlinearity followed by a multiple motion model. We begin by assuming that the input is a product of two moving signals, as in . The velocities of G and F are given by the vectors and . The main mathematical constraints arise from the spatiotemporal gradients of the logarithm of the input:

where is a product of two moving signals with velocities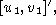 . If we apply the cascade of derivatives to the logarithm of the image I , we obtain the following differential constraint:

from equation ( 3 ), is the vector of measurements and the vector of unknowns. We will use the notation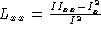 etc. for brevity.

To the model, the number of independent measurements required is 5. Two components to take into account the aperture problem for each transparent surface, and a final component obtained from the mixed term ( ). This final constraint is required to determine the correct combination of velocities[ 10 ]. The velocities may be solved from the vector of unknowns by:

If we bandpass filter before the logarithmic transformation, then the transformation is frequency selective. This frequency selectivity allows the model to detect additive motion transparencies[ 9 ]. However, this leads to a general concern with respect to the choice of the bandpass filter. For multiplicative transparencies, a narrowband filter may introduce distorsion into the processed image signal[ 5 ]. This is because multiplicative transparencies are potentially broadband stimuli. If the filter is broadband, then we cannot detect additive transparencies. Therefore a compromise must be sought, but this issue is not considered here.

Detecting transparency to plaids is interesting because there are only two linearly independent constraints. To see this note that there are only two frequencies with non-zero power, and in principle, a coherent interpretation always exists mathematically, despite the common forms of transparency that are often perceived. Because they have only 2 degrees of freedom, these stimuli produce a degenerate system of equations. The unknowns in equation (2) could be solved by dynamic programming using nonlinear inequality constraints like:

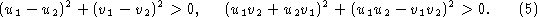
However, it is unclear whether this approach will yield the feasible solutions that are required from local computations. As an alternative, we exploit the principle that velocity parallel to the orientation of a 1-d structure is zero. This leads to the linear system:

and four equations. Summing the two off-diagonal elements gives:

Each of the above equations have two degrees of freedom. Their collection leads to an over determined system (although one is always redundant) and the detection of motion transparency. To calculate the confidence measure to transparency, each constraint was assigned a Lagrange multiplier and then collected into a single least-squares system using the first two eigenvectors from an SVD (appendix A). From this, the geometric mean to the eigenvalues of the regression matrix was determined and normalised. An example of this is given by equation ( 21 ).

   
Figure 2: Artificial Neural Networks for transparent motion detection. The motion network is equivalent to equation ( 9 ). (B) A 3-flow transparent network. Extending the number of layers to the artificial neural network according to equation ( 12 ) allows the detection of three transparent velocities. The desired output of the network (D) is zero.