3 Experiments

The discriminatory powers of the three shape coding techniques are demonstrated on a data set that consists of 79 irregular objects (Figure 4 ). These objects are surface defects which are obtained from base paper samples via an unsupervised segmentation procedure [ 9 ]. The distribution of different shapes does not necessarily possess any distinct clusters. That is, one cannot tell when a class changes to another and any classification becomes impossible. More likely, different shape classes vary smoothly and are more suitably interpreted by continuous descriptors.

   
Figure 4: A set of 79 irregular objects used in experiments.

Each object was given as an ordered ( x , y ) presentation of the contour pixels. In case of the chain code histogram (CCH), each contour was first chaincoded with an 8-connected chain code and then the CCH was calculated. When forming the pairwise geometric histogram (PGH) the contours of all objects were first approximated with polygons. The curvature guided polygonal approximation algorithm proposed in [ 1 ] was used. The number of angles and distances was quantized to 8 levels. The 8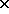 8 PGH was thus obtained. To further reduce the size of the PGH, conditional expectations of each row and column were calculated and collected to a 16-dimensional feature vector. In case of the five simple shape descriptors, each descriptor was calculated, normalized to [0,1], and put into a feature vector.

   
Figure 5: Sample contours on a self-organizing map. (a) The chain code histogram, (b) the pairwise geometric histogram, and (c) the set of five simple shape descriptors is used.

The self-organizing map (SOM)[ 11 ] is used to visualize the ordering of objects. In Figures 5 (a)-(c) are the SOMs which are trained with the three shape coding techniques. The previously mentioned data set of 79 irregular objects is used in training. If many objects are mapped to one map unit, only one object is depicted. All shape coding techniques seem to produce a logical ordering of objects. However, the ordering of objects with the chain code histogram is not as good as with other methods since the CCH cannot distinct between smooth and unsmooth objects. The pairwise geometric histogram and the simple shape descriptors seem to produce a very similar ordering. Smooth transitions from smooth to unsmooth objects and from circle-like to rod-like objects are nicely illustrated.

To further test the discriminatory powers of the three shape coding techniques a database retrieval problem is assumed. Three different shaped objects were selected as prototypes and the database (which consisted of 76 objects) was searched for three most similar objects. The prototypes and the retrieved objects are depicted in Figures 6 (a)-(c). The nearest retrieved object is at the top and the third nearest at the bottom of each column. The prototype object A is a thin rod-like object, the prototype object B is a smooth oval object, and the prototype object C is an unsmooth object. For the prototype object A the results are quite similar. Unlike the other descriptors the chain code histogram is not a rotation invariant descriptor. This results some differences in the results. For the prototype objects B and C the results are similar with the pairwise geometric histogram and with the simple shape descriptors. The chain code histogram cannot distinct between smooth and unsmooth objects.

   
Figure 6: Three most similar objects for three prototype objects retrieved from a database. (a) The chain code histogram, (b) the pairwise geometric histogram and (c) the set of five simple shape descriptors is used.