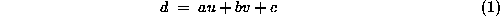
GPOD parameterises the ground plane using measurements of disparity. It includes an initial calibration stage in which the ground plane parameters are extracted from images of the ground containing line features but no obstacles. It then compares the disparity values in a new image pair with the expected ground plane disparity to detect differences (hence obstacles). The ground plane disparity d varies linearly with cyclopean image plane position [ 6 ], that is
where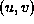
is the cyclopean image coordinates.
We obtain a least-squares fit for the ground plane parameters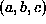
by orthogonal regression. However, as the image coordinates and the
measured disparities are not noise-free, we study the covariance of the
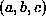estimate because this tells us how much confidence we can have in our
ground plane estimate.
Re-arranging Equation 1 , we have au+bv-d+c=0 , and so we minimise
where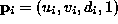
and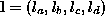
. The ground plane parameters
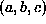are obtained as
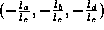. This problem is equivalent to
subject to
in which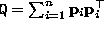
, i.e.
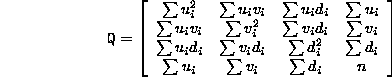
The Lagrangian for this is given by
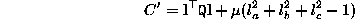
Setting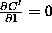
, we have
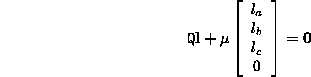
The solution for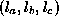
is the eigenvector corresponding to the least eigenvalue of the matrix
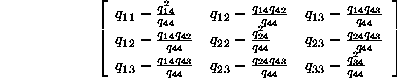
and
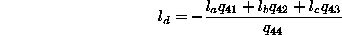
where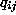
denotes the
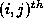element of matrix
.
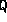The estimate of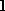
gives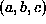
. Now we need to analyse the covariance of
. To do this, we follow the technique outlined in Faugeras [
3
] (pages 151-158) for the constrained minimisation case. Assuming that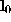
has been obtained by minimising the criterion function
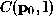subject to the constraint above, this defines implicitly a function
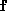such that
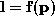in a neighbourhood of
.
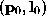We define the vector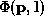
by
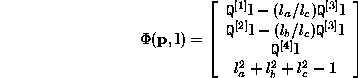
where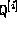
denotes the
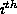row of matrix
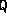. The Jacobian of
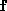is given by
Assuming that the error at each point is independent and that the errors
are isotropic, the covariance matrix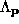
for the original data is block diagonal in form with
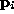's covariance matrix as the
block, assuming all points have the same diagonal covariance matrix,
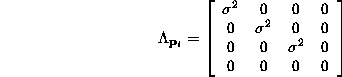
The covariance matrix for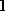
is given by
The ground plane parameters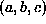
are obtained as
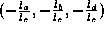, in which
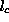is always close to unity and its variance is smaller than those of the
others by a magnitude of at least 2. For this reason, we take the
variances for
a
,
b
and
c
to be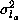
,
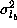and
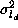respectively [
1
].
From Equation
1
, we can now determine the disparity variance, using the error
propagation formula for the product of two uncorrelated distributions [
1
] given by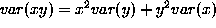
. We find that the expected disparity is
Stephen Se
