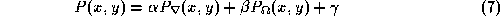



In the spirit of [ 1 ] we propose on-the-fly training for the most appropriate local potential of the form
While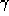 has no effect on the location of any extrema of
P
(
x
,
y
), it allows us to consider (
7
) as a single layer network with weights
has no effect on the location of any extrema of
P
(
x
,
y
), it allows us to consider (
7
) as a single layer network with weights ,
,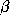 and
and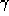 . We can then train the network using a pseudo-inverse [
2
] and training samples
. We can then train the network using a pseudo-inverse [
2
] and training samples gathered from around the boundary. We define target values for the
training samples as follows:
gathered from around the boundary. We define target values for the
training samples as follows:
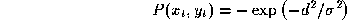
where
d
is the distance in pixels of from the boundary. Thus the target values are -1 on the boundary and
approach zero asymptotically away from the boundary. When trained,
P
(
x
,
y
) should have local minima on the segmentation boundary, as required.
Since we are training
local
boundary models,
from the boundary. Thus the target values are -1 on the boundary and
approach zero asymptotically away from the boundary. When trained,
P
(
x
,
y
) should have local minima on the segmentation boundary, as required.
Since we are training
local
boundary models, ,
,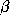 and
and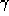 are calculated for each spline segment. We found that the performance of
the system was not sensitive to the parameter
are calculated for each spline segment. We found that the performance of
the system was not sensitive to the parameter , which we conveniently set to unity. We also found it advantageous to
discard the moduli signs in equation (
5
): this allows the algorithm to exploit the polarity of the boundary.
Note how on-the-fly training will automatically find the right sign for
, which we conveniently set to unity. We also found it advantageous to
discard the moduli signs in equation (
5
): this allows the algorithm to exploit the polarity of the boundary.
Note how on-the-fly training will automatically find the right sign for .
.
While such training is of no benefit for single-frame segmentation, it can greatly speed-up the process of segmenting many slices through a 3D data set. Since the boundary statistics generally change slowly from one slice to the next, optimal segmentation potentials ( 7 ) learned in one slice will also work well on the next slice. What emerges is a segmentation paradigm with the following structure:
 in slice 1. Initially, in the absence of any texture models, the snake's
potential function (
7
) is calculated with
in slice 1. Initially, in the absence of any texture models, the snake's
potential function (
7
) is calculated with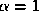 and
and .
. distributed evenly around its length. Corresponding target points
distributed evenly around its length. Corresponding target points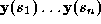 are located using a 1D search normal to the spline for a local minimum
of the potential (
7
).
are located using a 1D search normal to the spline for a local minimum
of the potential (
7
).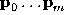 are adjusted to minimise
are adjusted to minimise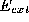 in (
1
).
in (
1
).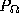 (one per spline segment) are calculated by sampling patches around the
boundary (Figure
3
) and using (
2
)-(
4
) and (
6
).
(one per spline segment) are calculated by sampling patches around the
boundary (Figure
3
) and using (
2
)-(
4
) and (
6
). ,
,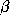 and
and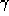 are calculated using training samples and a pseudo-inverse [
2
] such that
P
(
x
,
y
) in (
7
) is minimised at boundaries.
are calculated using training samples and a pseudo-inverse [
2
] such that
P
(
x
,
y
) in (
7
) is minimised at boundaries.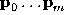 as a starting point in the new slice.
as a starting point in the new slice.



A.H. Gee