


Next:
3 Properties of boundaries
Up:
Adaptive Segmentation of Ultrasound
Previous:
1 Introduction
Active contours, or snakes [
10
] have found many applications in image analysis and computer vision. A
snake is a parametric contour , in the image plane (
x
,
y
). The snake evolves under internal and external ``forces'', usually
described by energy terms
, in the image plane (
x
,
y
). The snake evolves under internal and external ``forces'', usually
described by energy terms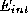 and
and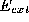 . The internal forces keep the snake smooth and the external forces
couple the snake to the image
I
(
x
,
y
), attracting the snake to features of interest (for segmentation
applications, these features would be object boundaries). The internal
forces usually take the form
. The internal forces keep the snake smooth and the external forces
couple the snake to the image
I
(
x
,
y
), attracting the snake to features of interest (for segmentation
applications, these features would be object boundaries). The internal
forces usually take the form
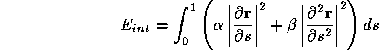
The term controls the ``tension'' of the snake while the
term controls the ``tension'' of the snake while the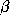 term controls its ``rigidity''. The external forces take a similar form:
term controls its ``rigidity''. The external forces take a similar form:
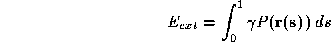
where
P
(
x
,
y
) is a scalar potential function designed so that local minima of the
function coincide with image features of interest. For instance, if we
are trying to detect boundaries which are characterised by high
intensity gradients, then a suitable potential would be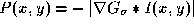 , where
, where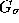 is a 2D Gaussian kernel with standard deviation
is a 2D Gaussian kernel with standard deviation pixels.
pixels.
Starting from an initial position, the snake evolves under the influence
of the combined field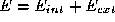 . In practical implementations, the snake is split into piecewise linear
segments and local forces are calculated at each vertex. The motion of
the snake is computed using gradient descent [
10
] or Lagrangian dynamics [
11
]. For segmentation applications, the idea is that the equilibrium
position of the snake provides the desired segmentation. If
I
(
x
,
y
) changes, the snake can also be used to
track
a boundary over time, providing motion as well as shape information [
3
].
. In practical implementations, the snake is split into piecewise linear
segments and local forces are calculated at each vertex. The motion of
the snake is computed using gradient descent [
10
] or Lagrangian dynamics [
11
]. For segmentation applications, the idea is that the equilibrium
position of the snake provides the desired segmentation. If
I
(
x
,
y
) changes, the snake can also be used to
track
a boundary over time, providing motion as well as shape information [
3
].
The main reason for using snakes in segmentation is that they allow the
incorporation of geometric constraints. In particular, they exploit (in
fact they rely on) prior boundary estimates obtained manually or from
the previous image in a sequence. Such an approach sensibly combines the
strengths of human operators (initial boundary
recognition
) and computer algorithms (accurate boundary
delineation
). Snakes have proved very successful for medical image segmentation [
12
]. In particular, snakes have been shown to give state-of-the-art
performance for segmenting intra-vascular ultrasound images [
4
].
An alternative way to enforce the smoothness constraint is to use cubic
B-spline snakes [
6
]. A cubic B-spline is specified by
m
+1 control points and comprises
m
-2 cubic polynomial curve segments
and comprises
m
-2 cubic polynomial curve segments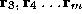 . The joining points between each curve segment are known as
knots
. The equation of each segment is \
. The joining points between each curve segment are known as
knots
. The equation of each segment is \
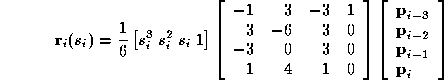
for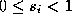 and
and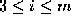 . For notational convenience we can re-parameterise the spline over a
single parameter
s
:
. For notational convenience we can re-parameterise the spline over a
single parameter
s
:

where are the spline basis functions and
are the spline basis functions and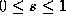 . The representation
. The representation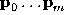 is more compact than the long list of vertices in piecewise linear
formulations. Moreover, the internal forces are no longer required: the
smoothness of the snake is implicit in the B-spline formulation.
B-splines may be open or closed as required, and are defined with
continuity properties at each knot. The flexibility of the curve
increases as more control points are added: each additional control
point allows one more inflection. It is also possible to use multiple
knots to reduce the continuity at knots [
14
].
is more compact than the long list of vertices in piecewise linear
formulations. Moreover, the internal forces are no longer required: the
smoothness of the snake is implicit in the B-spline formulation.
B-splines may be open or closed as required, and are defined with
continuity properties at each knot. The flexibility of the curve
increases as more control points are added: each additional control
point allows one more inflection. It is also possible to use multiple
knots to reduce the continuity at knots [
14
].
However, what makes B-splines especially useful for segmentation is that
they exhibit local control: modifying the position of one control point
causes only a small part of the curve to change. This leads to an
effective and simple algorithm for computing the motion of the snake
under the influence of image forces -- see Figure
1
. Local forces are computed at
n
sample points distributed evenly around the spline. At each sample point, a
one-dimensional search is performed normal to the spline for a local
minimum
distributed evenly around the spline. At each sample point, a
one-dimensional search is performed normal to the spline for a local
minimum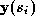 of
P
(
x
,
y
): we shall refer to the points
of
P
(
x
,
y
): we shall refer to the points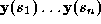 as
target points
. A force is applied at each sample point proportional to the distance
between the sample and the target points, ie:
as
target points
. A force is applied at each sample point proportional to the distance
between the sample and the target points, ie:
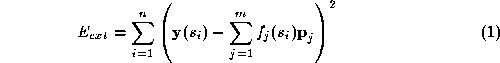
The positions of the control points are then updated to minimize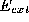 using linear least squares [
6
]. The one-dimensional search and re-estimation of the control points is
repeated until the snake attains equilibrium.
using linear least squares [
6
]. The one-dimensional search and re-estimation of the control points is
repeated until the snake attains equilibrium.
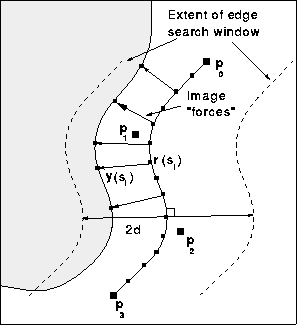
Figure 1:
B-spline snakes.
The snake evolves under a set of ``forces'' applied at a set of sample
points. Each force is proportional to the distance between the sample
point and the target point. The target point is found by a
one-dimensional search normal to the spline for an image feature of
interest. At equlibrium the snake provides a compact representation of
the boundary.
The main drawback of both piecewise linear and B-spline snakes is the
difficulty in specifying
a-priori
the correct smoothness parameters (ie. setting and
and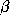 , or specifying the correct number of control points). Techniques have
been proposed to automatically introduce the ``best'' number of control
points [
5
], though such techniques tend to be computationally expensive. Here we
propose an extremely straightforward, novel work-around. We use a
B-spline formulation with a fairly small number of control points. While
this tends to give overly smoothed contours, we base our segmentation
not on the B-spline
, or specifying the correct number of control points). Techniques have
been proposed to automatically introduce the ``best'' number of control
points [
5
], though such techniques tend to be computationally expensive. Here we
propose an extremely straightforward, novel work-around. We use a
B-spline formulation with a fairly small number of control points. While
this tends to give overly smoothed contours, we base our segmentation
not on the B-spline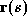 but on a piecewise linear contour with vertices
but on a piecewise linear contour with vertices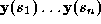 . The target points provide a good segmentation, while the B-spline
formulation constrains the search for the target points and therefore
stops the snake becoming too ``bent'' and intersecting itself.
. The target points provide a good segmentation, while the B-spline
formulation constrains the search for the target points and therefore
stops the snake becoming too ``bent'' and intersecting itself.



Next:
3 Properties of boundaries
Up:
Adaptive Segmentation of Ultrasound
Previous:
1 Introduction
A.H. Gee
Wed Jun 25 12:11:11 BST 1997
 , in the image plane (
x
,
y
). The snake evolves under internal and external ``forces'', usually
described by energy terms
, in the image plane (
x
,
y
). The snake evolves under internal and external ``forces'', usually
described by energy terms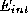 and
and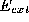 . The internal forces keep the snake smooth and the external forces
couple the snake to the image
I
(
x
,
y
), attracting the snake to features of interest (for segmentation
applications, these features would be object boundaries). The internal
forces usually take the form
. The internal forces keep the snake smooth and the external forces
couple the snake to the image
I
(
x
,
y
), attracting the snake to features of interest (for segmentation
applications, these features would be object boundaries). The internal
forces usually take the form


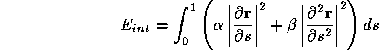
 term controls the ``tension'' of the snake while the
term controls the ``tension'' of the snake while the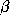 term controls its ``rigidity''. The external forces take a similar form:
term controls its ``rigidity''. The external forces take a similar form: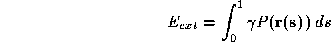
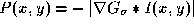 , where
, where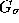 is a 2D Gaussian kernel with standard deviation
is a 2D Gaussian kernel with standard deviation pixels.
pixels.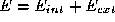 . In practical implementations, the snake is split into piecewise linear
segments and local forces are calculated at each vertex. The motion of
the snake is computed using gradient descent [
. In practical implementations, the snake is split into piecewise linear
segments and local forces are calculated at each vertex. The motion of
the snake is computed using gradient descent [ and comprises
m
-2 cubic polynomial curve segments
and comprises
m
-2 cubic polynomial curve segments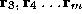 . The joining points between each curve segment are known as
knots
. The equation of each segment is \
. The joining points between each curve segment are known as
knots
. The equation of each segment is \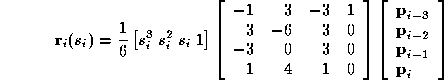
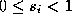 and
and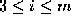 . For notational convenience we can re-parameterise the spline over a
single parameter
s
:
. For notational convenience we can re-parameterise the spline over a
single parameter
s
:
 are the spline basis functions and
are the spline basis functions and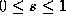 . The representation
. The representation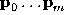 is more compact than the long list of vertices in piecewise linear
formulations. Moreover, the internal forces are no longer required: the
smoothness of the snake is implicit in the B-spline formulation.
B-splines may be open or closed as required, and are defined with
continuity properties at each knot. The flexibility of the curve
increases as more control points are added: each additional control
point allows one more inflection. It is also possible to use multiple
knots to reduce the continuity at knots [
is more compact than the long list of vertices in piecewise linear
formulations. Moreover, the internal forces are no longer required: the
smoothness of the snake is implicit in the B-spline formulation.
B-splines may be open or closed as required, and are defined with
continuity properties at each knot. The flexibility of the curve
increases as more control points are added: each additional control
point allows one more inflection. It is also possible to use multiple
knots to reduce the continuity at knots [ distributed evenly around the spline. At each sample point, a
one-dimensional search is performed normal to the spline for a local
minimum
distributed evenly around the spline. At each sample point, a
one-dimensional search is performed normal to the spline for a local
minimum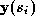 of
P
(
x
,
y
): we shall refer to the points
of
P
(
x
,
y
): we shall refer to the points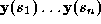 as
target points
. A force is applied at each sample point proportional to the distance
between the sample and the target points, ie:
as
target points
. A force is applied at each sample point proportional to the distance
between the sample and the target points, ie: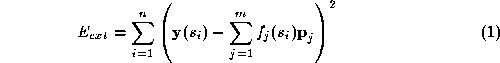

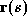 but on a piecewise linear contour with vertices
but on a piecewise linear contour with vertices