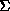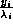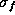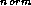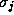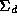Next:
6 Conclusions
Up:
Face Recognition in Dynamic
Previous:
4 Methods for face
In this section, experiments using Gaussian mixture models of identity
are described. Face image data were acquired and normalised in a fully
automated way by the face tracking system. The neural network model used
to perform tracking was trained using 9000 example face images rotated
by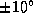 and scaled to
and scaled to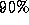 and
and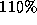 [
8
]. The normalised faces from the tracker therefore varied by at least
these amounts in scale and rotation. Since the aim of these experiments
was to compare methods for modelling identity rather than to optimise
recognition accuracy, no attempt was made to reduce these variations.
[
8
]. The normalised faces from the tracker therefore varied by at least
these amounts in scale and rotation. Since the aim of these experiments
was to compare methods for modelling identity rather than to optimise
recognition accuracy, no attempt was made to reduce these variations.
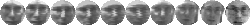 .........
.........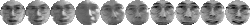
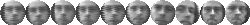 .........
.........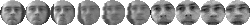
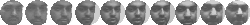 .........
.........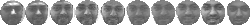
Figure 5:
Subset of data for subjects 5-7 (Left: training, Right: test).
Eight subjects were tracked through relatively unconstrained indoor
scenes as they walked towards a fixed camera. Overhead lighting resulted
in variations in facial illumination. The resolution of the area of the
face tracked ranged from approximately pixels when the subject was far from the camera to
pixels when the subject was far from the camera to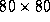 pixels when the subject approached the camera. Two normalised face
sequences were obtained for each subject. The first sequence of each
subject was used for training and the second sequence for testing. In
total, there were 326 training images and 296 test images. The number of
training images per person varied from 21 to 60 and the number of test
images from 21 to 53. Figure
5
shows 10 of the images used to form the training and test sets three of
the people.
pixels when the subject approached the camera. Two normalised face
sequences were obtained for each subject. The first sequence of each
subject was used for training and the second sequence for testing. In
total, there were 326 training images and 296 test images. The number of
training images per person varied from 21 to 60 and the number of test
images from 21 to 53. Figure
5
shows 10 of the images used to form the training and test sets three of
the people.
Face space was modelled by performing PCA on the training images. A
specific model was computed from the training set. A generic model was
computed using 644 of the images used to train a face detection neural
network in the tracking system. These images were highly suitable,
having similar variations in scale and rotation to the tracked data to
be recognised. The training images were projected onto the first
n
' eigenvectors and each person's identity was modelled by estimating
either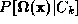 or
or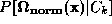 with Gaussian mixtures. The 8 mixture models' parameters were stored
along with the
n
' eigenvectors and eigenvalues and subsequently used to perform
classification of the test sequences.
with Gaussian mixtures. The 8 mixture models' parameters were stored
along with the
n
' eigenvectors and eigenvalues and subsequently used to perform
classification of the test sequences.
Initially, both a specific and a generic eigenspace were computed using
the first 40 eigenvectors. Table
1
shows a comparison of face classification using the specific and generic
models. Identities were modelled by fitting a single radial Gaussian to
each person's data. The percentage of images correctly classified for
each person along with the percentage of total images classified
correctly are given. Sequence classification results are also given
based upon a majority vote i.e. the sequence is classified as the person
with the most images. The result illustrates the fact that the use of a
generic face space which could be used to facilitate identity
verification, known/unknown or full recognition, in turn makes face
classification more difficult.
|
Face
|
Person (% images correct)
|
Total
|
Seq.
|
|
space
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
%
|
(Maj.)
|
|
Specific
|
75
|
64
|
74
|
85
|
56
|
78
|
29
|
11
|
55.1
|
7
|
|
Generic
|
57
|
67
|
66
|
20
|
13
|
72
|
25
|
29
|
43.6
|
4
|
Table 1:
Test set results with generic and specific face space models using 40
principal components. Identities were modelled by fitting a single
radial Gaussian to each of the 8 people.
A reduction in the dimensionality of the generic face space from 40 to
20 did not result in any significant loss of accuracy. Face
classification results using the 20-dimensional generic space are given
in Table
2
. Sequences were classified (1) by a majority vote (Maj.) and (2) by
accumulating probabilities (Pr.). Gaussian mixture models of various
complexity were compared for modelling identity.
The first two methods in Table
2
used unnormalised pattern vectors. The first method (T-P) used single
radial Gaussians of equal variance resulting in a nearest-mean
classifier which was equivalent to the eigenfaces method of Turk and
Pentland [
10
]. The second method was a nearest neighbour classifier (1-NN). Both
these methods performed poorly. However, the use of normalised pattern
vectors resulted in a significant improvement with T-P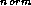 classifying 4 sequences correctly. The mixture models had either radial
or diagonal covariance Gaussians with between 1 and 3 components. A
mixture of 2 radial Gaussians provided the best performance.
classifying 4 sequences correctly. The mixture models had either radial
or diagonal covariance Gaussians with between 1 and 3 components. A
mixture of 2 radial Gaussians provided the best performance.



Next:
6 Conclusions
Up:
Face Recognition in Dynamic
Previous:
4 Methods for face
Shaogang Gong
Fri Jul 11 10:14:24 BST 1997
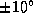 and scaled to
and scaled to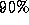 and
and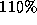 [
8
]. The normalised faces from the tracker therefore varied by at least
these amounts in scale and rotation. Since the aim of these experiments
was to compare methods for modelling identity rather than to optimise
recognition accuracy, no attempt was made to reduce these variations.
[
8
]. The normalised faces from the tracker therefore varied by at least
these amounts in scale and rotation. Since the aim of these experiments
was to compare methods for modelling identity rather than to optimise
recognition accuracy, no attempt was made to reduce these variations.


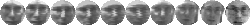 .........
.........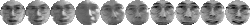
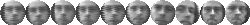 .........
.........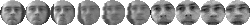
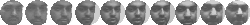 .........
.........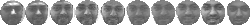
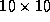 pixels when the subject was far from the camera to
pixels when the subject was far from the camera to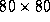 pixels when the subject approached the camera. Two normalised face
sequences were obtained for each subject. The first sequence of each
subject was used for training and the second sequence for testing. In
total, there were 326 training images and 296 test images. The number of
training images per person varied from 21 to 60 and the number of test
images from 21 to 53. Figure
pixels when the subject approached the camera. Two normalised face
sequences were obtained for each subject. The first sequence of each
subject was used for training and the second sequence for testing. In
total, there were 326 training images and 296 test images. The number of
training images per person varied from 21 to 60 and the number of test
images from 21 to 53. Figure 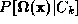 or
or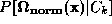 with Gaussian mixtures. The 8 mixture models' parameters were stored
along with the
n
' eigenvectors and eigenvalues and subsequently used to perform
classification of the test sequences.
with Gaussian mixtures. The 8 mixture models' parameters were stored
along with the
n
' eigenvectors and eigenvalues and subsequently used to perform
classification of the test sequences.