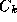 . A person's identity is modelled by estimating the class-conditional
density,
. A person's identity is modelled by estimating the class-conditional
density,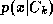 , from examples of that person's face. This density takes the form of a
mixture estimated using the EM algorithm described in section 2:
, from examples of that person's face. This density takes the form of a
mixture estimated using the EM algorithm described in section 2:


The approach proposed in this work provides a recognition framework that can be applied to any of the four tasks defined in Section 3. The main idea is to model a class-conditional density for each person in a representation space of relatively low dimensionality. Given such class-conditional densities, all four recognition tasks can be performed in a well-founded, statistical way. However, the method chosen to estimate these densities needs to be sufficiently general in order to model the highly non-convex distributions generated by different images of a face. It should also allow for a range of model complexity in order to model people for whom a relatively small amount of data are available. As more data are collected through recognition the model should be able to adapt to capture the underlying distribution more accurately.
The method selected here for density estimation was Gaussian mixture models. Modelling face classes with mixture models has several attractive characteristics. Density estimation is performed in a semi-parametric way so that the size of the model (number of mixture components) scales with the complexity of the data rather than with the size of the data set. The method is sufficiently general to model highly complex, non-linear distributions given enough data. However, it can also be constrained in a straightforward manner to obtain well-conditioned estimation given limited data. When classification is performed, other models emerge as special cases of using Gaussian mixtures, e.g. nearest neighbour and nearest mean classification.
Each person,
k
, constitutes a class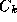 . A person's identity is modelled by estimating the class-conditional
density,
. A person's identity is modelled by estimating the class-conditional
density,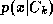 , from examples of that person's face. This density takes the form of a
mixture estimated using the EM algorithm described in section 2:
, from examples of that person's face. This density takes the form of a
mixture estimated using the EM algorithm described in section 2:
Appearance-based face representations usually have high dimensionality and in practice fitting a mixture of Gaussians is often highly under-constrained due to limited data and the ``curse of dimensionality''. There are, however, at least three complementary approaches to making the modelling tractable.
Firstly, the number of parameters in the model can be reduced by
constraining the form and the number of Gaussian mixture components. In
the most general case, each Gaussian,
j
, has a covariance matrix,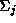 , which is completely determined by the data. If
, which is completely determined by the data. If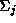 is constrained to be a diagonal matrix then there are only 2
d
parameters to be determined. If
is constrained to be a diagonal matrix then there are only 2
d
parameters to be determined. If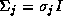 for some
for some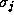 then the Gaussian is radially symmetric and there are only
d
+1 parameters to be determined. Finally, if
then the Gaussian is radially symmetric and there are only
d
+1 parameters to be determined. Finally, if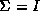 then only the mean must be estimated.
then only the mean must be estimated.
Secondly, the data set can be artificially enlarged by synthesising new virtual images for each person using models of possible variations of a face image. In its simplest form, this approach consists of applying a set of simple transformations to the images e.g. small translations, scalings, rotations and mirroring about the vertical axis. Noise can also be artificially added to the images. More complex models of deformation can also be employed for synthesis of virtual views, e.g. [ 1 ].
Thirdly, the dimensionality of the face representation vectors can be
reduced. A simple way to reduce dimensionality in the image domain is to
consider only a restricted part of the face and to reduce the image
resolution. A significant reduction in dimensionality is achieved by
representing faces as vectors in the subspace of faces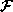 rather than as image vectors in the space of all possible images.
However,
rather than as image vectors in the space of all possible images.
However,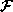 is difficult to model.
is difficult to model.
Since the intrinsic dimensionality of face space,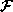 , is much less than that of the space of all images,
, is much less than that of the space of all images,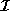 , a significant reduction in dimensionality can be obtained without loss
of significant information provided that two criteria can be met:
, a significant reduction in dimensionality can be obtained without loss
of significant information provided that two criteria can be met:
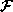 is accurately modelled in such a way that separability of identity is
preserved.
is accurately modelled in such a way that separability of identity is
preserved.
A representative data set containing a large number of different
identities is needed in order to build a
generic
model of the face space. In practice, a
specific
approximation,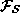 , is usually obtained from images in the set
, is usually obtained from images in the set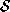 of
N
known people. When
N
is small,
of
N
known people. When
N
is small,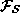 is a poor approximation to
is a poor approximation to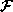 . If a specific model is used, it must be updated each time the set
. If a specific model is used, it must be updated each time the set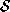 changes. Furthermore, any identity-specific models which make use of
changes. Furthermore, any identity-specific models which make use of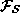 must also be updated. In contrast, a generic model need never be
updated. An important point here is that
face classification
is easier to perform in
must also be updated. In contrast, a generic model need never be
updated. An important point here is that
face classification
is easier to perform in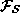 than in
than in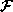 while
identity verification
,
known/unknown
and
full recognition
are best performed in a generic face space,
while
identity verification
,
known/unknown
and
full recognition
are best performed in a generic face space,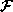 .
.
In theory, if exact pointwise correspondences can be established between all face images, face space can be accurately modelled using linear vector spaces [ 1 ]. In practice, establishing even a small set of feature correspondences between faces is highly problematic, especially at low resolution. In experiments described in section 5, only approximately aligned frontal or near-frontal views of faces are considered and linear models can provide reasonably accurate representation [ 6 ]. Principal Components Analysis (PCA) has been used to obtain face space models for face classification [ 10 ]. The models are computed without the use of any identity class information. PCA is therefore suitable for data sets with only a few example images per person and (or) large numbers of people. Linear discriminant analysis (LDA) has also been used (e.g. [ 4 ]). It is able to preserve class linear separability when applied to data sets with many images per person and relatively few people. It is therefore suitable for computing specific face space models for face classification using many training images of a few people.
In experiments described in the next section, a large data set containing many different people with only a few images per person was used to compute a generic face space using PCA. The next subsection gives a brief description of the PCA ``eigenface'' methods used.
Given
n
face images of size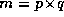 pixels, a face eigenspace is calculated as follows. Each image defines
an
m
-dimensional column vector
pixels, a face eigenspace is calculated as follows. Each image defines
an
m
-dimensional column vector . The mean,
. The mean,
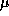 , and the
, and the covariance matrix,
covariance matrix,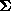 , of the set of
n
face images are computed. Let
, of the set of
n
face images are computed. Let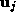 ,
,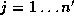 , be the
n
' eigenvectors of
, be the
n
' eigenvectors of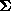 which have the largest corresponding eigenvalues
which have the largest corresponding eigenvalues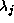 . The
n
' eigenvectors are the principal components. For an image,
. The
n
' eigenvectors are the principal components. For an image, , an
n
'-dimensional ``pattern vector'',
, an
n
'-dimensional ``pattern vector'',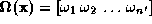 , can be computed by projection onto each of the eigenvectors
, can be computed by projection onto each of the eigenvectors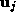 :
:
This pattern vector can be normalised by the eigenvalues in order to give the data equal variance along each principal component axis:
Class-conditional densities can be modelled in a principal subspace by
estimating either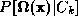 or
or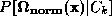 .
.



Shaogang Gong