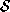Given a database consisting of a set,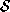
, of
N
known people, different face recognition tasks can be envisaged. Four
tasks are defined here as follows:
.
.
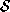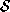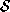, and if so to determine the subject's identity.
When considering appearance-based approaches to these tasks it is
helpful to know something of the topology of sets of face images in an
image space. The set of all faces forms a small number of extended,
connected regions
. Furthermore, a face undergoing transformations such as rotation,
scaling and translation results in a connected but strongly non-convex
subregion in the image space. Whilst these transformations might be
approximately corrected using linear image-plane transformations, large
rotations in depth, illumination changes and facial expressions cannot
be so easily ``normalised''. Therefore, the set of images of a single
face will form at least one and possibly several, highly non-convex,
connected regions in image space.
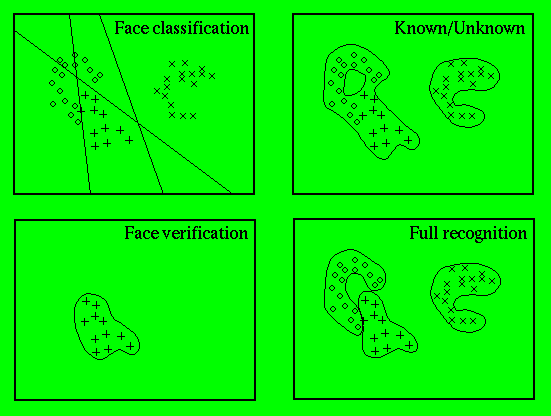
Figure 4:
Plotted in a hypothetical face space,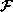
, are example faces from 3 different people. Suitable decision
boundaries are shown for the four recognition tasks.
Figure
4
illustrates the four recognition tasks defined above in a hypothetical
face space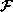
, where
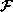is assumed to contain all possible face images and to exclude all other
images. Plotted in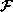
are example faces for three different people
. Suitable decision boundaries for performing the recognition tasks are
shown. The separability of face identities in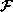
will depend upon the technique used to model
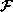. However, it is likely that each identity will form strongly non-convex
regions in this subspace. In the
face classification
task, all
N
classes can be modelled. In contrast, the other three tasks all suffer
from the need to consider the class of unknown faces. Each task will now
be discussed in greater detail.
The face classification task is an
N
-class classification problem in which all
N
classes can be modelled. It can be tackled by collecting representative
data for each of the
N
classes and applying one of many possible pattern classification
techniques. The probability of misclassifying a face
x
is minimised by assigning it to the class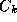
with the largest posterior probability
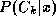, where
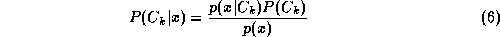
p
(
x
) is the unconditional density,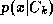
is the class-conditional density and
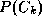is the prior probability for class
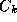. Since
p
(
x
) is the same for every class it need not be evaluated in order to
maximise posterior probability [
3
]. Therefore, one approach to the classification task is to model the
class-conditional probability densities,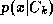
, for each class. This approach is explored in this work. An alternative
approach is to estimate discriminant functions using e.g. Linear
Discriminant Analysis (LDA) [
4
].
Face verification can be treated as a 2-class classification problem.
The two classes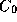
and
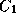correspond to the cases where the claimed identity is true and false
respectively. In order to maximise the posterior probability,
x
should be assigned to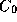
if and only if
Density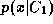
represents the distribution of faces other than the claimed identity.
This is difficult to model but a simple assumption is that it is
constant over the relevant region of space, falling to zero elsewhere.
In this case, Inequality (
7
) is equivalent to thresholding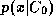
. Perhaps a more accurate assumption is that the density
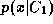is smaller in regions of space where
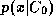is large. If
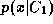is chosen to be of the form
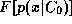, where
F
is a monotonically decreasing function, then this assumption is also
equivalent to thresholding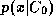
. In this case, the threshold takes the form
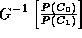, where
. Since
G
is monotonic,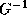
is unique
. Utilising only data from class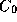
, it is therefore reasonable to perform verification by thresholding
.
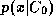In order to achieve more accurate verification, negative data, i.e. data
from class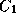
, would need to be used in order to better estimate the decision
boundaries. Only data which are ``close'' to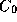
are relevant here. An iterative learning approach can be used in which
incorrectly classified unknown faces are selected as negative data.
Furthermore, the face images used to train the face detection network
also provide a suitable source of negative examples for identity
verification [
8
].
This task can also be treated as a 2-class classification problem. The
two classes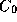
and
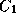correspond to the cases where the subject is and is not a member of the
known group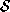
, respectively. The methods discussed above for face verification can be
similarly applied to this 2-class problem.
A slightly different approach involves building an identity verifier for
each person in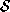
. The known/unknown task is performed by carrying out
N
identity verifications. If the numerator in the threshold of Inequality (
7
) is the same for all verifiers then they can be combined in a
straightforward manner.
The full recognition task can be performed by combining N identity verifiers similarly to the second approach described above for known/unknown.
Shaogang Gong
