Next: 5 Experimental Results and Up: Visual Tracking of Solid Previous: 3 Solid Objects
Next:
5 Experimental Results and
Up:
Visual Tracking of Solid
Previous:
3 Solid Objects
The object pose is inferred by aligning the geometric model of an object to the estimated silhouette in the images (1D set of B-spline control points) given an estimated pose. The initial object pose in the first frame is assumed to be known, enabling the computation of the silhouette and initializing the contour tracker. Afterwards, the silhouette is tracked through the image sequence and repeated pose estimation is used to update the state of the 3D pose tracker.
Before we formulate the problem, we have to define what we henceforth
understand under the term ``object''. Objects are connected, bounded
3-manifolds embedded in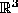
. Let
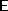be the set of all objects, then
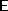together with the Hausdorff metric
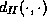is a metric space. The group
G
of 3D Euclidean transformations has six degrees of freedom and maps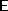
onto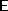
. The orbit of a single object
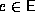under
G
:
is a 6-dim manifold in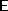
. It is parameterized by
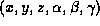, where (
x
,
y
,
z
) are the translation parameters and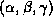
are the rotation angles around the x, y, and z-axis
. Consider an object model
and a realization
, then the pose estimation problem can be stated as: Determine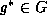
, such that
:
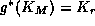The problem has not a unique solution for all objects, e.g. for a sphere
always exists a 3D manifold of solutions. Let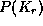
be the weak perspective image of the object
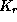. Then the optimization problem (
1
) can be reformulated:
where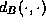
is defined on
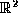, obeying the condition:
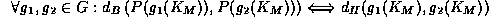
stating that if the silhouettes are equal, the objects have to be equal,
too. For tracking tasks the condition can be restricted to an (open)
neighborhood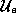
of an object
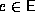, since an estimate
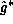of the object pose is available. The condition becomes:
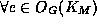exists an open neighborhood
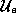such that
:
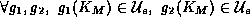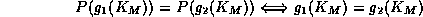
Under this condition the function
exhibits a global minimum at the point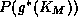
, where
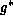is the solution to the problem (
2
).
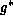can be determined by searching for the global minimum.
It remains to define the metric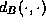
, but instead of choosing the Hausdorff metric on
,
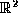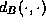is defined as the symmetric area difference between the graphs of
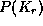and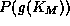
:
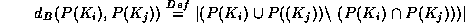
Since the measured as well as the estimated silhouettes computed from
the 3D object model are represented as B-splines, the area difference of
the graphs can be efficiently computed by intersecting the splines and
symbolically integrating along the curves (using the Gauss Theorem for
integration over curves in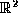
).
As already pointed out, the silhouette of an object cannot be expressed
as an analytical function of the 3D object model. Hence, there is no
closed form solution to the optimization problem (
2
). The optimization is executed in subgroups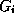
of the transformation group
G
, where the silhouettes have to be represented invariant with respect to
the unknown parameters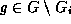
. The B-splines can be represented translation and
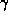-rotation invariant by computing the first and second order moments
. To achieve invariance, the B-splines are translated to align their
center of gravity with the coordinate origin, scaled to unit area and
rotated, such that the mixed second moment vanishes.
At first the parameters
and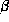
are computed by determining the function
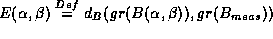at discrete points in the open neighborhood of the predicted pose
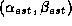, where
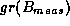is the graph of the normalized measured silhouette and
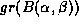denotes the graph of the normalized silhouette of the object at
.
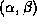is computed on a regular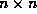
grid with center
.
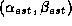The global minimum of
can be computed by fitting a quadric to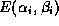
,
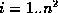. The coefficients
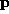of the quadric are computed by minimizing the square error difference,
setting up the normal equation. The inverse of the normal equation
matrix can be computed off-line, if the grid is previously translated to
the origin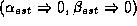
. The position of the minimum
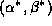can be extracted from
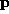by partially differentiating the quadric and setting the gradient to
zero.
The third angle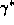
can be computed using
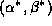by again fitting a quadratic function to the symmetric area differences
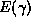measured at discrete points in the neighborhood of
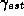, or by simply taking the differences in the normalization angles
computed from the second order moments, which leads to ambiguities
solvable by comparing with the predicted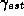
. The translation parameters
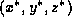can also be recovered from the normalization parameters.
The object pose derived from the silhouette is likely to be erroneous.
For pose smoothing and prediction a Kalman filter is derived with the
state vector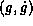
, where
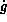represents the linear and angular velocity of the parameters
g
, respectively.
After an aspect change occurred, new control points may have to be introduced in the contour tracker to model corners or curved parts of the silhouette invisible in the previous aspect. As a consequence, a contour state estimate has to be derived, including an estimate of the control point velocity. These image velocities can be estimated from the 3D object pose velocity.
At first aspect changes which influence the shape of the silhouette are predicted to reinitialize the contour tracker. An aspect change is determined by certain visual events (see Koenderink et al. [ 8 ] for a complete list of visual events). For smooth objects aspect changes influencing the silhouette are restricted to T-junction events, which can be discovered by comparing the topological structure of T-junctions of different silhouettes. Furthermore, if the difference between the currently utilized template in the contour tracker and the predicted silhouette exceeds a certain threshold, the template has to be replaced by a new (set of) silhouettes.
