Next: 4 Tracking the 3D Up: Visual Tracking of Solid Previous: 2 Active Contour

3 Solid Objects

Object Representation

The surface of a smooth, curved object can be described by a finite collection of parametric surface patches pieced together to form a composite surface. A single patch can be efficiently represented as (uniform) B-spline tensor product surface:

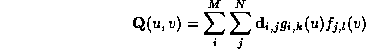
defined on a (rectangular) parametric region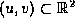 , where 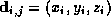are the control points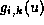, and and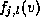 are B-spline basis functions of order k and l , respectively. For basis functions of order three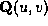 is a piecewise biquadratic function with positional and first parametric derivative continuity at the boundary between the segments (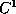 continuity). 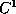continuity at the border between two (biquadratic) tensor product surface is easily achieved by interpolating the control points at the border of the patches, choosing equal control points at the border and assuring, that three control points across the border (with the common border control point being the midpoint) are collinear.

Objects of genus 0 cannot be described by rectangular surface patches only. Triangular patches can be designed for inclusion by choosing identical control points at one side of a tensor product surface or by using 3-valent polynomial surfaces.

Silhouette

To determine the object's silhouette we compute the preimage of the contour in the parametric regions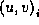 of the surfaces i first. This is a subset of the singular points of the mappings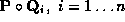 , where P is the weak perspective projection, and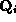 is the i-th tensor product surface. 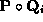maps the points of the parametric region i into the image plane. For biquadratic B-spline tensor product surfaces the singular points, characterized by a vanishing Jacobian, are the solutions of a 5th order algebraic equation.

If the singular points have to be computed, the structure of these curves and the visual events which might occur, have to be considered. Presuming a smooth mapping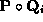 , then according to [ 13 ] the mapping is good, if the gradient of the Jacobian does not equal zero in any point of the parametric region: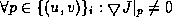 . In this case the singular points form smooth, non-intersecting curves in the parametric region, called general folds. The curves can be computed using a curve trace algorithm for the algebraic equation based on Newton's method. The algorithm is initialized with the singular points computed at the border of the parametric regions.

If the mapping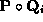 is not good in a finite number of isolated points, stating that the gradient might vanish, a visual event of codimension 1 occurred . The curves of singular point can only be traced from the regions border toward those points. The existence of those points can numerically be checked while approaching them, although their occurrence is in practice very seldom.

The curves formed by singular points are implicitly linked across the border of parametric regions through the curve tracing. Once these curves are pointwise approximated, they can be mapped into the image plane via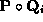 and are denoted by .

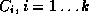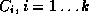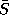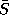The silhouette is a subset of the contour, consisting of one or more closed curves. To compute the outer curve, the intersections and self-intersections of have to be computed. The outer curve is determined and intersection points (representing T-junctions) are explicitly marked. After a chord length parameterization, is approximated with a closed, quadratic B-spline by minimizing the square distance between the B-spline and the curve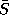 . T-junctions are explicitly modeled as corners in the spline.