Next: 3 Solid Objects Up: Visual Tracking of Solid Previous: 1 Introduction
Next:
3 Solid Objects
Up:
Visual Tracking of Solid
Previous:
1 Introduction
The method used to track an object silhouette in an image sequence is
based on
a framework for spatiotemporal control of the tracking of visual
contours
[
2
].
A contour is efficiently represented in parametric form as a closed
B-spline (
X
(
s
),
Y
(
s
)):
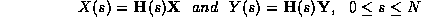
where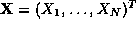
and
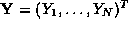are the control point vectors and
is a vector of basis functions. In our tracking framework
are chosen
depending on the shape
of the contour, which is approximately known in advance, enabling
efficient contour tracking. More specifically, spline segments can be
linear or quadratic
for linear and curved contour parts, respectively. Furthermore, corners
in the silhouette arising from vertices at the object surface or from
T-junctions are modeled as corners in the spline
.
The contour is assumed to evolve over time with a uniform 2D motion,
where randomly varying forces acting on the contour are modeled as an
additive Gaussian noise process. In an augmented state space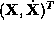
,
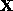representing the position and
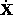the velocity, a simple dynamic model can be introduced as a stochastic
differential equation:
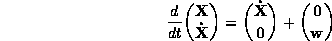
where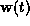
is a zero mean, temporally uncorrelated noise process. A similar
equation applies for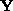
. The
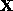and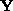
processes are independent, assuming isotropic noise processes.
The B-spline contour represents the current estimate of the real silhouette, which can be measured in the images as contrast edges . Measurements of the visual feature are made in the normal direction along the B-spline contour at sample points. The measurements are then used to update the current B-spline contour.
A steady state Kalman filter is derived to enhance the tracking process according to the assumed underlying motion model of the contour. A detailed discussion of the spatio-temporal filtering can be found in [ 2 ] and [ 12 ].
The expected shape of the visual feature in the first frame is used to initialize the system state of the contour tracker. However, its influence decreases continuously, so that, in a steady state Kalman filter, no shape memory remains. For tracking silhouettes of 3D rigid objects it is desirable to assure, that the tracker retains some shape memory throughout the tracking process by means of a persistent template. A persistent template enforces additional smoothness on the B-splines. Furthermore, the tracker should not only be attracted to the initial template, but to a set generated by a certain group of transformations on the template, in order to account for the transformations a 3D rigid object (and hence its silhouette) might undergo in space.
The contour generator of a curved object is viewpoint dependent, which makes it impossible to regard it as a rigid space curve and utilizing the persistent template suggested in [ 10 ]. However, due to the availability of the 3D pose tracker we are able to predict the silhouette in the future. For small viewpoint changes we can then approximate the allowed silhouette changes by linear combinations of the current and future silhouettes. This can be integrated in the tracking framework by restricting the state space onto a subspace spanned by a few silhouettes.