


Next: 2 Active Contour Up: Visual Tracking of Solid Previous: Visual Tracking of Solid



Next:
2 Active Contour
Up:
Visual Tracking of Solid
Previous:
Visual Tracking of Solid
Visual tracking of known, solid objects as they move in space has been extensively studied, since it is a crucial prerequisite for solving tasks in robotics, biomedical image analysis, autonomous navigation and surveillance.
Certain assumptions and constraints about the shape and motion of the objects, as well as about the environment have been imposed to be able to solve the task or to reduce its complexity. In all these attempts computational efficiency is still one of the most critical points to measure the success of a vision system designed to solve a task.
If the object pose has to be tracked based on image contours, we have to distinguish between approaches appropriate for polyhedra and those for curved objects. For polyhedra the image contours are projections of stationary edges at the objects surface. Correspondences between the object surface and the image features can be established to solve for the unknown pose parameters. However, this approach fails for curved objects, because the contour generator (or rim) is not stationary, but slides over the surface as the object moves. Hence, no point-to-point correspondence can be easily made between object surface and image points. In [ 7 ] is shown, that a point-to-curve correspondence can be found between special image points, such as inflection or bitangent points, and curves at the objects surface, such as parabolic or bitangent curves. However, model and image features are not of the same dimensionality and object positioning is not easily made.
An explicit model of a polyhedron can be projected onto the image plane to align the model features (edges and vertices) to the image features to determine the pose. Recognition via alignment has been successfully implemented in a number of systems. Applying this approach to tracking is straightforward, using the estimated pose of the last processed frame as initial pose for a new frame. For instance in [ 6 ] objects are explicitly described by 3D polyhedra and used for tracking the full pose, in real time.
Dickinson et al. [ 5 ] proposed a method to qualitatively track the appearance of a polyhedral object using an active contour network (snakes). With this network the geometry of the occluding contour is tracked, but no geometric knowledge about the object is exploited. On a symbolic level topological distinct views of an object are clustered in an aspect graph to determine the object aspect and to control the contour network, i.e. to change the topology of the network. Since no geometric object model is used, the object pose and motion can be determined only qualitatively and aspect changes can only be detected, but not predicted.
In our framework the 3D object geometry is used for model based contour tracking as well as for deriving the full object pose by solving the (weak) inverse perspective transformation based on point correspondences. Aspect changes are predicted to count for tracking robustness. The tracking results of our framework applied to polyhedra were presented in [ 10 ]. Here we will concentrate on smooth curved objects.
Most research in curved object recognition has focused on segmenting the image into volumetric primitives, which can directly be compared to volumetric descriptions of objects. Examples include quadrics, superquadrics, and generalized cylinders, which are recovered from range or intensity data. Little emphasis has been given to the recognition of objects, with the exception of [ 3 ]. Besides this, only a limited class of objects can be described by volumetric primitives and more complicated objects have to be assembled by parts.
Curved objects can be represented as a collection of image contours seen from different viewpoints. Since the contour generator of curved objects is view point depending, image contours of nearby views can deviate significantly. In [ 1 ] the objects are represented by a small set of silhouettes and 3D surface curvature and depth is attached to each silhouette point to avoid large sets of views. Using the surface curvature of points along the silhouette a new silhouette can be predicted by applying a certain transformation. However, the new silhouette is computed pointwise and accurate predictions are only made for umbilic and parabolic points.
Using the curvature method, Stockman et al. [ 4 ] presented a method for recovering and tracking the pose of curved objects. A new silhouette of the model object is predicted using the curvature method. A similarity measure for the image and the model silhouettes is defined and the pose parameters are determined by applying Newton's method for non-linear least square minimization. The method is computationally expensive and the estimated pose deviates up to 20 degree from the true values. The model set is verbose and the alignment of the model to the 2D data must proceed iteratively.
In [ 9 ] the use of algebraic surfaces as object models is suggested. The image observables (image intensity, range or contour points) are explicitly related to the geometric model for recognition and pose estimation. The intermediate step to predict the object appearance and match the image observables to features of the same dimensionality is bypassed. Elimination theory provides a method to construct a single implicit equation, that relates the image observables to the object shape and viewing parameters. Determining the pose parameters is reduced to a non-linear least square minimization of a polynomial equation in the image observables and the pose parameters.
In the experiments the image observables are segmented by hand. Since segmentation and recognition are in general tightly coupled problems, it remains open how the image segmentation could proceed. Experiments are presented for object surfaces described by a single algebraic surface, e.g. a torus, where it takes about 24 seconds to align the torus to an image. For complex surfaces represented by a collection of algebraic surfaces no algorithm is given for assigning the image observables to the different surfaces patches (since for an image observable only one implicit equation describing a particular algebraic surface must equal zero) and estimating the common object pose.
In [ 7 ] smooth surfaces are represented by high order tangency (HOT) curves, a discrete, non-parametric representation anchored by differential geometry. Given a viewpoint, points on the parabolic curves and on the bitangent developables, which are additionally rim points, project to inflection and bitangent points detectable in the images. From a number of such points invariants can be computed, which can be used for subsequent pose estimation and object recognition. The image contours for detecting inflection and bitangent points are extracted by edge detection and linking in the image, computing differential properties especially in the case of inflection points is not very accurate. Inflection and bitangent points are spurious points on the silhouette and geometric information of most silhouette parts are not exploited. Recognition of a single object takes about 30 seconds [ 7 ].
The system consists of the following components (see figure 1 ):
The 2D contour tracker pursues the silhouette represented as a B-spline through an image sequence. For stability, a 2D curve, provided by the 3D pose tracker, is used as a template, where the silhouette is expected to lie within the orbit of the curve with respect to the 2D affine transformation group. After processing an image, the current estimated shape and position of the silhouette is transmitted to the pose tracker. The 3D object pose is derived from the 1D set of measurements, the B-spline control points, using a geometric 3D model of the object. Based on the estimated object pose and the object model, the pose tracker predicts aspect changes and significant deviations of the template from the currently estimated silhouette and triggers the appropriate control of the contour tracker, e.g. assigning a new template if needed.
The object is viewed under weak perspective projection. There is no object recognition method implemented prior to the tracking stage, the initial object pose in the first frame is assumed to be known.
In the following section we outline the 2D contour tracker implementation. Section 3 describes the 3D object model we are using, and in section 4 the 3D pose tracker is explained. We present experimental results in section 5 and conclude.
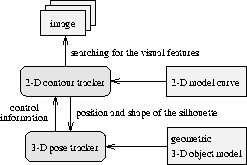
Figure 1:
Components of the tracking system


