


Next:
3 View Interpolation for
Up:
Video Mosaicing using Manifold
Previous:
1 Introduction
A common method for construction of panoramic mosaics includes the
collection of sections (``strips'') from each image and pasting these
strips next to each other to become the mosaic. In the simple case of a
camera which is moving horizontally, vertical strips are taken from each
image and pasted side by side [
11
] (see Fig.
1
.a). This process can also be viewed as scanning the scene with a
vertical broom [
4
,
16
]. This vertical broom scans the entire sequence, extracts vertical
strips along the sequence, and pastes them one next to the other to
create the panoramic mosaic. The vertical broom is perpendicular to the
horizontal optical flow, and after placing the strips in the panoramic
image, the optical flow is pointing exactly to the direction from which
the panoramic image is constructed (see Fig.
1
.b).

Figure 1:
The relation between the mosaicing process using strips and the
direction of the optical flow.
(a) The simple case of camera which is moving to the left. The optical
flow points to the right, and vertical strips are collected. After
pasting, The optical flow is parallel with the direction in which the
panoramic image is built.
(b) New information is passing through the scanning broom when the
Optical Flow is perpendicular to the broom.
(c) No new information is passing through the scanning broom when it is
parallel to the optical flow.
(d) When the scanning broom is set to be perpendicular to a radial
optical flow its shape will be a circular arc.
The scanning broom must be perpendicular to the optical flow. A counter
example is shown in Fig.
1
.c, using a vertical scanning broom with vertical optical flow. When the
optical flow is parallel to the scanning broom no mosaic is created as
no new information will pass through the broom. The case where the
scanning broom is perpendicular to a radial optical flow is shown in
Fig.
1
.d. The information from all images in the sequences will pass through
the scanning broom, allowing to collect strips for pasting in the
mosaic.
The following section describes a practical implementation for
determining the shape of the scanning broom for the case of affine
motion, which can give good approximation for image motion in many
cases. Numerous methods exist to recover the parameters of an affine
transformation [
7
,
13
]. Implementations for other motion models can be done in a similar
manner.
The affine transformation can be expressed as:

where and
and are corresponding points in images
are corresponding points in images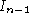 and
and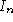 , and the parameters of the affine transformation
, and the parameters of the affine transformation are (
a
,
b
,
c
,
d
,
e
,
f
). (
u
,
v
) is the optical flow vector as a function of the position
are (
a
,
b
,
c
,
d
,
e
,
f
). (
u
,
v
) is the optical flow vector as a function of the position . The transformation
. The transformation (and the optical flow) vary continuously along the sequence.
(and the optical flow) vary continuously along the sequence.
The scanning broom will be a line such that it will be perpendicular to the optical flow. The normal to
the line
such that it will be perpendicular to the optical flow. The normal to
the line is in the direction
is in the direction thus it should be in the same direction as (
u
,
v
). This constraint can be expressed by:
thus it should be in the same direction as (
u
,
v
). This constraint can be expressed by:

for some value of
k
. A line equation can be derived by integration only when
e
=
c
. In most cases, the difference between the values of
c
and
e
is due to the rotation around the optical axis , such that it contributes
, such that it contributes to
c
, and
to
c
, and to
e
. To approximately satisfy the condition
e
=
c
it is therefore sufficient to rotate the image by
to
e
. To approximately satisfy the condition
e
=
c
it is therefore sufficient to rotate the image by after the affine transformation is recovered, and then recompute the
affine transformation.
after the affine transformation is recovered, and then recompute the
affine transformation.
After correction for rotation around the optical axis, when the affine
transformation is such that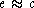 , we get the following equation of the scanning broom by integration:
, we get the following equation of the scanning broom by integration:

This is a family of lines that are all perpendicular to the optical
flow.
M
is used to select a specific line. We suggest that
M
will be set to the value for which the line contains maximum number of
pixels within the image. If many options exist, then we suggest using a
line as close as possible to the center of the image to minimize lens
distortions. This selection should ensure that pixels used in the mosaic
will be from that image having best resolution at that location.
We will use the following notation to describe the scanning broom along
the sequence: The line is the line in Image
is the line in Image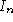 , in it's coordinate system, which corresponds to the affine
transformation
, in it's coordinate system, which corresponds to the affine
transformation . This affine transformation
. This affine transformation relates points
relates points in Image
in Image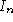 to corresponding points
to corresponding points in Image
in Image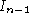 (see Fig.
3
).
(see Fig.
3
).
Eq.
3
can be easily understood for some simple cases.
-
In the case of a uniform horizontal optical flow (either a small pan or
a sideway translation), the affine transformation
 takes the form
takes the form , thus the selected broom becomes
, thus the selected broom becomes , which is a vertical line (see Fig.
2
.a).
, which is a vertical line (see Fig.
2
.a). -
In the case of a uniform vertical optical flow (either a small tilt or a
vertical translation), the affine transformation takes the form
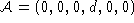 , thus the selected line becomes
, thus the selected line becomes , which is a horizontal line (see Fig.
2
.b).
, which is a horizontal line (see Fig.
2
.b). -
In the case of zoom or forward motion (towards a planar surface which is
parallel to the image plane), the affine transformation takes the form
 , where
b
is the scaling factor (
f
=
b
). As a result, the selected broom becomes
, where
b
is the scaling factor (
f
=
b
). As a result, the selected broom becomes , which is a circle around the center of the image (see Fig.
2
.c).
, which is a circle around the center of the image (see Fig.
2
.c).
For pure camera translations the scanning broom will be a circle around
the Focus of Expansion (FOE). In more general cases the scanning broom
may be approximated by an elliptic curve.

Figure 2:
Examples for scanning broom.
(a) A vertical scanning broom is selected for horizontal motion.
(b) A horizontal scanning broom is selected for vertical motion.
(c) A circular scanning broom is selected for zoom and for forward
motion.
The mosaic is constructed by pasting together strips taken from the
original images. The shape of the strip, and its width, depend on the
image motion. This section describes how to determine these strips in
the case of an affine motion to conform with the methodology of the
selection of best resolution. Strip selection for other motion models
can be done in a similar manner.
In order to determine the strip to be taken from Image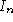 , the preceding frame,
, the preceding frame,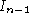 , and the succeeding frame,
, and the succeeding frame, , should be considered. Let
, should be considered. Let be the affine transformation relating points
be the affine transformation relating points in Image
in Image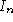 to the corresponding points
to the corresponding points in Image
in Image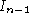 , and let
, and let be the affine transformation relating points
be the affine transformation relating points in Image
in Image to the corresponding points
to the corresponding points in Image
in Image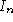 .
.
Given the affine transformations and
and , the lines
, the lines and
and are selected respectively (see Fig.
3
.a-c). The line
are selected respectively (see Fig.
3
.a-c). The line in
in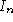 corresponds to the line
corresponds to the line in
in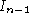 using the affine transformation
using the affine transformation . In the same way, the line
. In the same way, the line in
in corresponds to the line
corresponds to the line in
in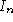 using the affine transformation
using the affine transformation .
.
The strip that is taken from the image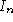 is bounded between the two lines
is bounded between the two lines and
and in
in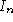 (see Fig.
3
.a-c).
(see Fig.
3
.a-c).
Using this selection, the first boundary of the strip will be described
by the selected line , thus will be exactly orthogonal to the optical flow with regard to the
previous image. The second boundary of the strip is described by the
line
, thus will be exactly orthogonal to the optical flow with regard to the
previous image. The second boundary of the strip is described by the
line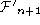 which is the projection of the line
which is the projection of the line onto the current image
onto the current image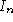 , having the same property in the next image.
, having the same property in the next image.
This selection of the boundaries of the strip ensures that no
information is missed nor duplicated along the strip collection, as the
orthogonality to the optical flow is kept.
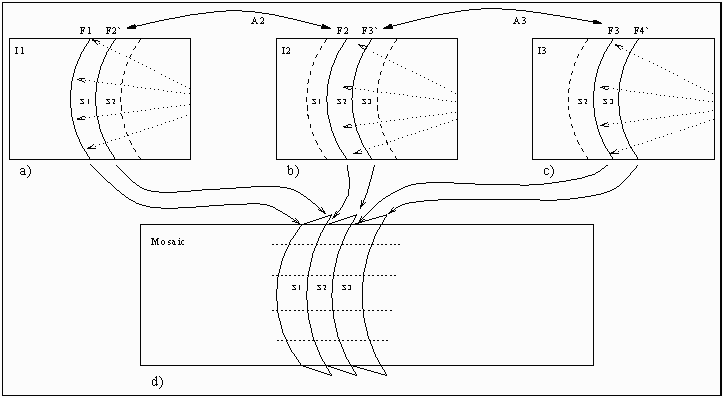
Figure 3:
Example of cutting and pasting strips.
(a)-(c) Strips are perpendicular to the optical flow. Line is selected in Image
is selected in Image and Line
and Line is selected in Image
is selected in Image . The mapping of Line
. The mapping of Line (in
(in ) into Image
) into Image using the affine transformation is Line
using the affine transformation is Line . The strip
. The strip taken from Image
taken from Image is bound between lines
is bound between lines and
and .
.
(d) Strips are warped and pasted so that the optical flow becomes
parallel, their back is fixed (e.g. in Strip
in Strip ) and their front (e.g.
) and their front (e.g. in Strip
in Strip ) is warped to match the back of the next strip.
) is warped to match the back of the next strip.
To create continuous mosaic images while avoiding accumulated
distortions, the warping of the strips should depend only on the
adjacent original frames, independent of the history of previous
distortions. This section describes how to warp the strips in the case
of affine motion.
In our scheme, the back of each strip is never changed. This is the side
of the strip which corresponds to the boundary between Image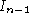 and Image
and Image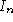 and defined by
and defined by . The front of the strip is warped to match the back side of the next
strip. This is the boundary between Image
. The front of the strip is warped to match the back side of the next
strip. This is the boundary between Image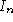 and Image
and Image which is defined by
which is defined by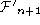 .
.
In the example described in Fig.
3
.d, we warp the first strip such that its left side does not change,
while its right side is warped to match the left side of the original
second strip. In the second strip, the left side does not change, while
the right side is warped to match the left side of the third strip, etc.
As a result, the constructed image is continuous. Also, if we warp the
original optical flow as we did with the strips, the resulting flow will
be parallel to the direction in which the panoramic mosaic is
constructed. Moreover, no accumulative distortions are encountered, as
each strip is warped to match just another original strips, avoiding
accumulative warps.
The strips as pasted in the example of Fig.
3
remain curved. The transformation can be modelled by a projection into a
cylindrical manifold, in which case the strips should be un-bent into
straight edges before pasting into the mosaic. Un-bending the strips may
cause distortions in some parts of the mosaic, and before visual
presentation the mosaic should be re-bent depending on the desired
viewpoint. The bending and un-bending, however, is not very critical
when the strips are curved only slightly.



Next:
3 View Interpolation for
Up:
Video Mosaicing using Manifold
Previous:
1 Introduction
Adrian F Clark
Thu Jul 24 15:12:24 BST 1997





 and
and are corresponding points in images
are corresponding points in images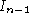 and
and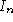 , and the parameters of the affine transformation
, and the parameters of the affine transformation are (
a
,
b
,
c
,
d
,
e
,
f
). (
u
,
v
) is the optical flow vector as a function of the position
are (
a
,
b
,
c
,
d
,
e
,
f
). (
u
,
v
) is the optical flow vector as a function of the position . The transformation
. The transformation such that it will be perpendicular to the optical flow. The normal to
the line
such that it will be perpendicular to the optical flow. The normal to
the line is in the direction
is in the direction thus it should be in the same direction as (
u
,
v
). This constraint can be expressed by:
thus it should be in the same direction as (
u
,
v
). This constraint can be expressed by:
 , such that it contributes
, such that it contributes to
c
, and
to
c
, and to
e
. To approximately satisfy the condition
e
=
c
it is therefore sufficient to rotate the image by
to
e
. To approximately satisfy the condition
e
=
c
it is therefore sufficient to rotate the image by after the affine transformation is recovered, and then recompute the
affine transformation.
after the affine transformation is recovered, and then recompute the
affine transformation.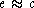 , we get the following equation of the scanning broom by integration:
, we get the following equation of the scanning broom by integration:
 is the line in Image
is the line in Image . This affine transformation
. This affine transformation relates points
relates points in Image
in Image in Image
in Image , thus the selected broom becomes
, thus the selected broom becomes , which is a vertical line (see Fig.
, which is a vertical line (see Fig. 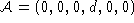 , thus the selected line becomes
, thus the selected line becomes , which is a horizontal line (see Fig.
, which is a horizontal line (see Fig.  , where
b
is the scaling factor (
f
=
b
). As a result, the selected broom becomes
, where
b
is the scaling factor (
f
=
b
). As a result, the selected broom becomes , which is a circle around the center of the image (see Fig.
, which is a circle around the center of the image (see Fig. 
 , should be considered. Let
, should be considered. Let in Image
in Image in Image
in Image be the affine transformation relating points
be the affine transformation relating points in Image
in Image are selected respectively (see Fig.
are selected respectively (see Fig.  in
in in
in , thus will be exactly orthogonal to the optical flow with regard to the
previous image. The second boundary of the strip is described by the
line
, thus will be exactly orthogonal to the optical flow with regard to the
previous image. The second boundary of the strip is described by the
line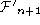 which is the projection of the line
which is the projection of the line onto the current image
onto the current image
 is selected in Image
is selected in Image and Line
and Line is selected in Image
is selected in Image . The mapping of Line
. The mapping of Line . The strip
. The strip taken from Image
taken from Image