


Next:
5 Conclusions
Up:
Face Recognition with the
Previous:
3 Continuous n-tuple classifiers
The continuous n-tuple classifier was tested on the Olivetti Research
Laboratory (ORL) database, available from
http://www.orl.co.uk/facedatabase.html
. The database consists of four hundred images: ten each from forty
people. Each image is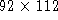 pixels, with the face filling most of the image, or in same cases being
cropped to fit the image. The images show considerable variation in
expression and angle to the camera, and some variation in the size of
the face as it appears in the image. For the subjects who wear glasses,
there are in some cases images with and without glasses.
pixels, with the face filling most of the image, or in same cases being
cropped to fit the image. The images show considerable variation in
expression and angle to the camera, and some variation in the size of
the face as it appears in the image. For the subjects who wear glasses,
there are in some cases images with and without glasses.
The database has been widely used by other researchers, as summarised
below, which makes it a useful benchmark.
To measure the accuracy of the method, a number of experiments were made
using the continuous n-tuple, the standard n-tuple and the nearest
neighbour method. Each of these results reported in the table is the
mean of 5 experiments. For each experiment the set of images was
randomly partitioned into disjoint training and test sets, with 5 images
of each person used for training and the remaining 5 for testing.
Experiments were made with different values of
n
and
m
, but the best performance was found with
n
= 4 and
m
= 500, both for the continuous and the standard n-tuple methods, and
these are the results quoted in Table
5
.
The continuous n-tuple method also works reasonably well for smaller
values of
n
and
m
- for example with
n
= 3 and
m
= 200 the continuous n-tuple has a mean error rate of 4.8%. Note that
conventional n-tuple methods are extremely simple to implement in
hardware, and this simplicity holds for the continuous n-tuple method,
providing that the continuous system can be compiled into conventional
n-tuple look-up tables. In the table the results quoted for ``cont
n-tuple*'' are for the compiled version on the continuous n-tuple
system, using 8 levels of quantisation. This still achieves a
respectable 4.2% error rate, while retaining the recognition speed of
the conventional n-tuple method, though the memory requirements are
greater, with an address space for each class of .
.
|
METHOD
|
Error rate (%)
|
Trianing Time
|
Classification Time
|
|
PDBNN
|
4.0
|
20min
|
<0.1s
|
|
SOM+CN
|
3.8
|
4hours
|
<0.5s
|
|
Top-down HMM
|
13.0
|
n/a
|
n/a
|
|
Pseudo-2d HMM
|
5.0
|
n/a
|
240s
|
|
Eigenface
|
10.0
|
n/a
|
n/a
|
|
n
-tuple
|
14.0
|
0.9s
|
0.025s
|
|
cont n-tuple
|
2.7
|
0.9s
|
0.33s
|
|
cont n-tuple*
|
4.2
|
30min
|
0.025s
|
|
1-nearest-neighbour
|
3.7
|
0s
|
1s
|
Table 5:
Error rates on the test data together with training and classification
times for the ORL database. Cont n-tuple* indicates the compiled version
of the continuous n-tuple with 8 levels of quantisation. All results
quoted in the table use five images per class for training and the
remaining 5 per class for testing. The various n-tuple results and
1-nearest-neighbour classifier are the mean of 5 experiments, each one
based on a different random partition of the data. The other quoted
results were gained using various different experimental methodologies;
hence, this table should only be taken as a rough guide.
Table
5
shows the performance of several different approaches on the ORL
database. The probabilistic decision-based neural net (PDBNN) results
are taken from Lin and Kung [
5
]. Self-organising map combined with convolutional neural net (SOM+CN)
results, together with the results of Eigenface, Top-down HMM and
Pseudo-2d HMM are taken from Lawrence
et al
[
4
] and Samaria and Harter [
10
]. The humble nearest neighbour classifier actually performs
surprisingly well. This is based on a city-block distance; a Euclidean
distance version performs significantly worse. The question of the
statistical significance of these difference arises, and it will be
interesting to explore this further, but from the results gained so far,
the continuous n-tuple system appears to be at the very least
competitive with the best of the other methods.
The timing results in Table
5
should be treated with some caution since the different methods have
been implemented by different people and on different platforms. The
timings for the various n-tuple classifier and the nearest-neighbour
method are based on a Java implementation running on a 200 MHz Pentium
PC.
An investigation was made into how the test-set error-rate varied for
the continuous and the standard n-tuple classifier with respect to the
number of samples used for training. In order to speed things up, values
of
n
= 3 and
m
= 200 were used. The results are shown in Figure
2
. Again, each point on the graph is the mean of five experiments, each
experiment based on a different random partition of the data.

Figure 2:
The variation of the test set error rate with respect to the number of
samples used for training for the continuous n-tuple classifier
(cont-n-tuple) and the standard n-tuple classifier (n-tuple). For both
systems, values of
n
=3 and
m
=200 were used. This gives poorer results than with
n
=4 and
m
=500 for example, but allows the experiments to be run more quickly, and
exhibits the same trend. Each point on the graph represents the mean of
5 experiments, with error bars plus/minus 1 standard deviation from the
mean. Each experiment used a different random partition of the data set,
and a different set of randomly chosen n-tuples.



Next:
5 Conclusions
Up:
Face Recognition with the
Previous:
3 Continuous n-tuple classifiers
Adrian F Clark
Thu Jul 24 16:25:40 BST 1997
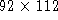 pixels, with the face filling most of the image, or in same cases being
cropped to fit the image. The images show considerable variation in
expression and angle to the camera, and some variation in the size of
the face as it appears in the image. For the subjects who wear glasses,
there are in some cases images with and without glasses.
pixels, with the face filling most of the image, or in same cases being
cropped to fit the image. The images show considerable variation in
expression and angle to the camera, and some variation in the size of
the face as it appears in the image. For the subjects who wear glasses,
there are in some cases images with and without glasses.


 .
.