Next: Stereo matching by SVD Up: Uncalibrated Stereo Correspondence Previous: The correspondence problem

The Scott and Longuet-Higgins algorithm

In a landmark paper [ 8 ], Scott and Longuet-Higgins proposed a neat, direct way of associating features of two arbitrary patterns. The algorithm exploits some properties of the singular value decomposition (SVD) to satisfy both the exclusion and proximity principles set forth by Ullman. A remarkable feature of the algorithm is its straightforward implementation founded on a well-conditioned eigenvector solution which involves no explicit iterations .

In the following, a brief description of the algorithm is given along with a simple experiment that illustrate its intrinsic usefulness. The reader is redirected to the original paper [ 8 ] for further theoretical and philosophical insights.

Let I and J be two images, containing m feature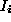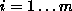s ( ) and n features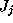 ( ), respectively, which we want to put in one-to-one correspondence. The algorithms consists of three stages.

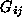1. Build a proximity matrix G of the two sets of features where each element is Gaussian-weighted distance between two features 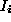and :
    
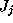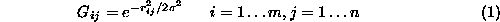
   where is their Euclidean distance if we regard them as lying on the same plane.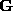 is positive definite and a 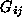decreases monotonically from 1 to 0 with distance. The parameter controls the degree of interaction between the two sets of features: a small value of enforces local interactions, while a larger value permits more global interactions.
2. Perform the singular value decomposition (SVD) of :
   
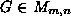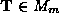   where and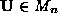 are orthogonal matrices and the diagonal matrix contains the (positive) singular values along its diagonal elements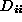 in descending numerical order. If m < n , only the first m columns of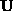 have any significance [ 8 ].
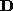3. Convert to a new matrix 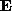obtained by replacing every diagonal element 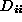with 1 and then compute the product
   
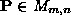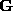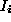   This new matrix has the same shape as the proximity matrix and has the interesting property of sort of ``amplifying'' good pairings and ``attenuating'' bad ones: `` if is both the greatest element in its row and the greatest element in its column, then we regard those two different features and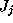 as being in 1:1 correspondence with one another; if this is not the case, it means that feature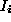 competes unsuccessfully with other features for partnership with 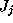'' [ 8 ].

It is not difficult now to figure out that this apparently simple method embeds both the proximity and the exclusion principle: the former one is a consequence of the nature of the proximity matrix and the latter arises from the orthogonality of the matrix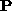 . In fact ``the fact that the squares of the elements in each row of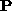 must add up to 1 implies that a given feature 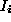cannot be strongly associated with more than one feature 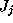. The mutual orthogonality of the rows tends to keep different features in the first image from becoming closely associated with the same feature in the second image'' [ 8 ]. Moreover,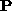 is a matrix which effectively produces a minimum squared distance mapping , since by applying the algorithm the trace of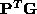 is maximized [ 8 ].

Although not mentioned in the original paper, the algorithm is rooted into the solution of the subspace rotation problem known as orthogonal Procrustes problem (see e.g. [ 2 ]).

As an example, the figures above show the mapping found by this algorithm for two hand-input patterns representing two scaled and translated ``A''s (circles and crosses); the overall mapping is extremely good and, as claimed, the proximity principle is defied in favor of a more globally consistent mapping. Scott an Longuet-Higgins show that the algorithm copes nicely with translation, shearing and scaling deformations and with moderate rotations (as in our visual system) and suggest criteria for the choice of the distance .

To my best knowledge, thus far only two (similar) works appears to have used the startling properties of this algorithm, namely [ 7 ] and [ 9 ], where the method was applied to matching modes of variation of finite element shapes, and in [ 5 ], where applications were suggested in eigen-shape fitting. The following section explains why the method as is does not fare as it could in real image matching situations and proposes a simple but key improvement on the nature of the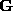 matrix.