



This paper advocates using color to enhance ATR systems. Color imagery offers a number of advantages: (i) the data is inexpensive to obtain (color cameras are cheap and freely available, and many prototype research vehicles are equipped with them), (ii) we have developed methods for real-time target detection shown to be effective under most naturally occurring daytime conditions, and (iii) the system can be easily combined with systems based on IR (or other sensory) data for even more reliable performance.

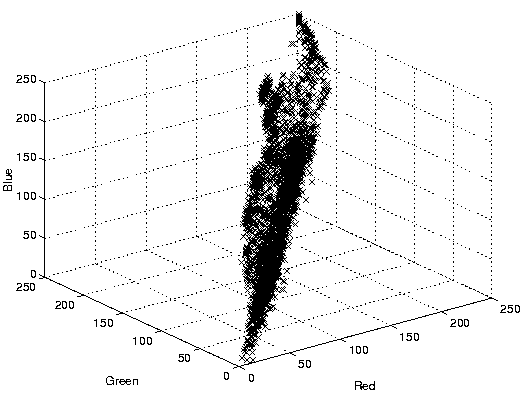
Figure 2:
(From top) Sample target; Target color (
RGB
) in a single outdoor image (sample extracted from vehicle hood);
Variation of apparent color over several hundred images in a single day.
While color can be a useful feature for target detection, there are several issues that complicate the use of color for recognition, especially in outdoor images. One clear disadvantage of using color (or any other feature from the visible spectrum) for ATR is that it cannot be used at night, in thick smoke or fog, or any conditions under which the targets are not visible. Additionally, there are other problems inherent to outdoor color imagery that further complicate color-based recognition.
The apparent color of an object is a function of the color of the incident light, surface reflection, illumination geometry, viewing geometry and imaging parameters [ 9 ]. Each of these factors can vary in outdoor conditions; in addition, the effect of a host of unmodeled phenomena, such as shadows and inter-reflections, is unpredictable. Consequently, at different times of the day, under different weather conditions, and at various positions and orientations of the object and camera, the apparent color of an object can be different. Figure 2 shows a camouflaged military vehicle, with its apparent color in RGB space in a single image (a small number of points in RGB) and the variation over 100 images in one day.
The variation in the color of daylight is caused by changes in the sun-angle, cloud cover, atmospheric haze and other weather conditions. The illumination geometry in a scene determines the orientation of the surface with respect to the two components of the illuminant, sunlight and (ambient) skylight, and hence the color of the incident light. Viewing geometry, i.e., the position and orientation of the camera with respect to the surface, determines the amount and composition of the light reaching the camera, depending on the specular content of the surface. Shadows and inter-reflections also affect the color of the light incident upon a surface [ 8 ]. Shadowing occurs either when the surface is facing away from the sun (self-shadowing), or when a second object blocks the sunlight. Inter-reflections are caused when other surfaces reflect light incident upon them, onto the surface in question. In both cases, the color of the incident light (and hence the apparent color of the surface) is affected. A number of imaging parameters cause further color shifts. For instance, wavelength-dependent displacement of light rays by the camera lens onto the image plane due to chromatic aberration can cause color mixing and blurring [ 14 ]. Nonlinear camera response and digitization errors can skew the ratio of the values in the three color bands (red, green and blue), and the dynamic range of intensity in outdoor scenes accentuates the possibility of blooming and clipping [ 14 ].
In the past, color recognition under varying illumination has generally been addressed as a color constancy problem, where the goal is to match object colors under varying illumination without knowing the spectral composition of the incident light or surface reflectance. An illuminant-invariant measure of surface reflectance is recovered by first determining the properties of the illuminant from variations across images. Unfortunately, in order to separate illumination conditions from surface reflectance effects, most color constancy algorithms make strong assumptions about the nature of the world. For example, Forsyth [ 7 ] assumes a Mondrian world with constant illumination without inter-reflections or multiple light sources; Finlayson [ 6 ] assumes that surfaces with the same reflectance have been identified in two spatially distinct parts of the image, and that the unknown illumination falls within the gamut of known artificial illuminants; Ohta [ 16 ] assumes artificial illumination constrained by the CIE model to reduce performance errors; Novak and Shafer [ 15 , 18 ] assume a point light source and pure specular reflection; Buchsbaum [ 3 ] assumes that the surface reflectance averaged over the entire image is grey; Maloney's work [ 12 ] is a refinement of Buchsbaum's but has been applied only under the constraints of an indoor world with Munsell color chips. While many of these constancy algorithms are quite sophisticated and perform impressively within the specified constraints, Forsyth [ 7 ] aptly states, ``Experimental results for [color constancy] algorithms running on real images are not easily found in the literature...Some work exists on the processes which can contribute to real world lightness constancy, but very little progress has been made in this area.''
According to the standard model of image formation [ 9 ], the observed color of objects in images is a function of (i) the color of the incident light (daylight), (ii) the reflectance properties of the surface of the object (iii) the illumination geometry, (iv) the viewing geometry, and (v) the imaging parameters. Theoretical parametric models exist for the various phases of the image formation process [ 9 , 10 , 13 , 18 ], although these models appear too restrictive to be used in unconstrained imagery; still, they provide an approximate qualitative description of the variation of apparent color. The CIE model [ 10 ] states that the color of daylight varies along a characteristic curve, defined by the following equation in the CIE chromaticity space (of which is a linear transform).
y = 2.87x - 3.0x^2 - 0.275.....................................................(1)
where 0.25 <= x <= 0.38. In RGB space, the parabola stretches out into a thin curved surface [ 4 ].
The effect of illumination geometry and viewing geometry depend on the reflectance of the surface. Most realistic surfaces have reflectances that have a mixture lambertian and specular components. Existing reflectance models of mixed reflection surfaces [ 9 , 13 , 18 ] are yet be applied to unconstrained imagery in the context of color-based recognition. We can, however, deduce from the CIE model and the reflection models, that the RGB distribution representing apparent color variation of a surface under daylight will lie along (a) a thin continuous curved volume if the surface is purely lambertian or purely specular, (b) a single blob if the surface has mixed reflection with a dominant lambertian component, and (c) two distinct clusters if the surface has mixed reflection with a dominant specular component.
The goal of imaging systems is to preserve the color of objects as they appear in the scene, depending on a few imaging parameters (focal length, response function, etc.). Unfortunately, phenomena such as clipping, blooming and nonlinearities will introduce distortions to the appearance of objects in color space [ 14 ].
Even if we assume that the distortions to the RGB distributions due to unmodeled parameters are not drastic, in the absence of precise and robust models of the various processes involved (as is the case with outdoor color images), the only assumption that can be made is that the RGB distributions representing the color of objects can be arbitrarily shaped.



Shashi Buluswar