 be the projection on the image plane of a 3-D point,
be the projection on the image plane of a 3-D point,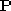 . In the camera frame, we let
. In the camera frame, we let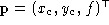 and
and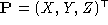 , and write
, and write


In this section we show that the motion field equations can be written in a strikingly simple form in terms of the coordinates of the epipole on the image plane. We consider a full-perspective, pinhole camera; since we are interested in the uncalibrated case, we shall use the screen reference frame (image points, coordinates in pixel) along with the usual camera reference frame (points in space, coordinates in millimiters), in which the optical axis is the Z axis, the optical center is the origin, and the image plane's equation is Z = f , with f the focal length.
We first establish some necessary notations. Let be the projection on the image plane of a 3-D point,
be the projection on the image plane of a 3-D point,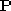 . In the camera frame, we let
. In the camera frame, we let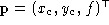 and
and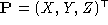 , and write
, and write

Assuming exact orthogonality between the horizontal and vertical axis of the camera, the same equations can be rewritten in the screen frame as
with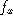 and
and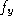 the focal length in horizontal and vertical pixel size, respectively,
and
the focal length in horizontal and vertical pixel size, respectively,
and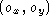 the coordinates of the image center in the screen frame. In what follows
we shall also use the ratio
the coordinates of the image center in the screen frame. In what follows
we shall also use the ratio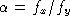 , sometimes called
aspect ratio
. If the camera is uncalibrated, the four
intrinsic parameters
,
, sometimes called
aspect ratio
. If the camera is uncalibrated, the four
intrinsic parameters
,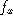 ,
,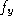 ,
,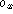 , and
, and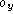 (and hence the aspect ratio) are unknown.
(and hence the aspect ratio) are unknown.
The 3-D motion of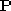 can be described by the 3-D vector
can be described by the 3-D vector
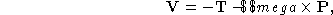
where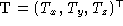 and
and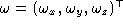 are the translational and angular velocity of
are the translational and angular velocity of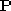 , respectively. The vectors
, respectively. The vectors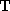 and
and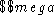 are sometimes called the
extrinsic parameters
. In components,
are sometimes called the
extrinsic parameters
. In components,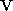 reads
reads
If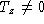 , the epipole,
, the epipole,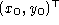 , is given in the screen frame by
, is given in the screen frame by
From Equation ( 3 ) a simple but important fact follows, that the knowledge of the epipole's location is equivalent to the reconstruction of the translation direction only in the calibrated case .
The motion field, , can be obtained by taking the familiar time derivative of Equations (
1
):
, can be obtained by taking the familiar time derivative of Equations (
1
):
By means of ( 1 ), ( 2 ) and ( 3 ), Equation ( 4 ) can be rewritten as
with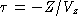 and
and
The equivalence of Equations ( 4 ) and ( 5 ) can be verified by expanding ( 4 ), according to ( 2 ), and ( 5 ) according to ( 6 ), ( 1 ), ( 2 ), and ( 3 ).
The structure of the motion field as unveiled by Equation (
5
) is remarkably simple. The parameters ,
,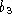 ,
,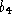 , and
, and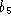 depend on both the intrinsic and extrinsic parameters, but not on the
3-D structure. Since the epipole is also independent of the 3-D
structure,
all the information on the 3-D structure of the observed scene is
contained in the term
depend on both the intrinsic and extrinsic parameters, but not on the
3-D structure. Since the epipole is also independent of the 3-D
structure,
all the information on the 3-D structure of the observed scene is
contained in the term
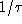 , which can be regarded as the inverse of a
generalized time-to-impact
.
, which can be regarded as the inverse of a
generalized time-to-impact
.
Before studying in detail the possible use of Equation ( 5 ), it is interesting to notice that this simple expression for the motion field has been obtained because, if the intrinsic parameters are unknown, the location of the epipole is not sufficient to reconstruct the direction of translation, and thus cannot be used to separate the translational and rotational components of the motion field.



Adrian F Clark