The process of evaluating a corner's orientation in our approach mainly
involves finding the orientation of the surrounding edges that form the
corner. Extracting such information is therefore essentially a local
process. We define a function
that signifies the likelihood of a pixel being part of the edges
associated with a particular corner C. The value of
is computed at each point
in a small neighbourhood around what has been labelled as a corner point
C. The following assumptions about the configuration within corners are
used:
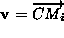
To satisfy the first assumption, we introduce the product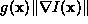
as a good edge detector. The mere gradient would be inconsistently
strong at noise spikes, and the mere anisotropism would be misleadingly
high on strongly orientated patterns such as a gradient intensity ramp.
Therefore, the combination of two identifies edges properly. We will
regard the direction of anisotropism
to be the direction of the edge points found.
The second assumption is necessary to deal with the problem of corner
adjacency. Several edges may be found in the neighbourhood of a corner,
they might not all belong to the same structure. Indeed, they could be
associated with another corner nearby. If the direction of an edge pixel
does not point toward the corner point C, then its value of
should be very low. To enforce this, we have introduced the angle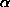
.
with
u
being the direction of anisotropsim at
, derived from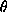
in Equation (
2
), and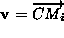
. As shown on figure
2
,
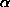is a measure of the difference between the direction of an edge at a
pixel
and the direction of
.
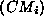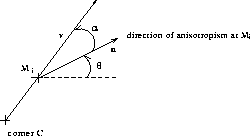
Figure 2:
Definition of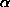
. C is a corner pixel,
is a point located within its neighbourhood.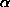
is the angular difference between the direction
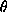of anisotropism at
and the direction of
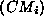
Computing the cosine of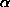
provides a good discriminant to establish which neighbouring corner an
edge point belongs to. Figure
3
illustrates this property: an edge point M is close to two different
corner points. When studying the neighbourhood of one of these corners,
is discarded, because the direction of the edge it belongs to is not
compatible with the direction of
.
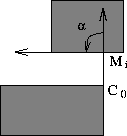
Figure 3:
Adjacent corners: when studying corner
,
is discarded, for at
Based on the remarks made above, we subsequently obtain an analytical
expression of
:
with n being a parameter controlling how strictly direction compatibility should be enforced. In our application, we used the value n =3.
To assist further understanding of Equation (
7
), Figure
4
gives a schematic summary of the main fields computed. (a) represents
the original image of a corner (b) shows anisotropism g(
x
), (c) shows cornerness c(
x
) and (d) shows the value of
in a small window around the corner point. Only the pixels belonging to
relevant edges are retained.
Figure 4:
a) Example image I(
x
) of a corner. An un-related edge is located within its neighbourhood.
b) Anisotropism g(
x
): the edges are strongly orientated along one direction whereas the
corner point is not. c) cornerness
. d)
: identification of the side points associated with the corner. The edge
that is not associated with the corner is discarded.
For each corner point C, the value of
is computed within a small neighbouring window
and a histogram H is constructed.
will be small. This automatically removes them from the histogram.
Figure
5
illustrates this in the case of a junction: the value of
is very small at the junction point whereas the three edges strongly
influence the histogram H.
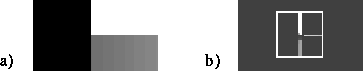
Figure 5:
a) Image of a junction. b) Value of
in a neighbourhood
. No orientation information is extracted from the junction point. The
arms are clearly identified.
The orientations of the arms of the corners are estimated by taking the
local maxima of the histogram. Each maximum is found in the
neighbourhood of a peak corresponding to one arm of the corner. A
technique has been designed to determine the number of peaks,
i.e.
, the number of edges defining the corner: two for a simple corner,
three or more for a junction. It is worth noting that care must be taken
when defining the size of
. Making it too small may not provide enough information for an accurate
estimation of the orientation. Making it too big would not be
computationally expensive but it would include irrelevant information in
the search process. Indeed, the corners we identify here are
extrapolated but not interpolated like with a Hough transform approach.
F. Chabat
