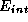 encouraging mesh tension and rigidity; an image term,
encouraging mesh tension and rigidity; an image term, , that attempts to differentiate between bone and non-bone and thus
enables a boundary to be delineated, and an inflating or ballooning
term,
, that attempts to differentiate between bone and non-bone and thus
enables a boundary to be delineated, and an inflating or ballooning
term,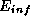 that forces the mesh towards the object boundary.
that forces the mesh towards the object boundary.


A comprehensive survey of the use of deformable models in medical image analysis can be found in [ 6 ]. Our deformable surface is defined as a closed triangular mesh which approximates the surface of the image feature being segmented. The vertices of the mesh triangles, the model nodes, correspond with voxels in the volume being segmented.
The segmentation process is formulated as the minimisation of a cost
function, and the behaviour of the model is determined by local cost
functions associated with each node. The three types of cost assigned to
each node are: an internal energy,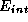 encouraging mesh tension and rigidity; an image term,
encouraging mesh tension and rigidity; an image term, , that attempts to differentiate between bone and non-bone and thus
enables a boundary to be delineated, and an inflating or ballooning
term,
, that attempts to differentiate between bone and non-bone and thus
enables a boundary to be delineated, and an inflating or ballooning
term,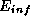 that forces the mesh towards the object boundary.
that forces the mesh towards the object boundary.
The initial mesh is an icosahedron which approximates a sphere and comprises 12 nodes. From this mesh, the model expands or `grows' outwards under the influence of the inflation force. Boundaries indicated by the image energy and the constraints imposed by the internal energy prevent the model growing out of the image feature.
The total energy of the model, , is determined at the
N
nodes, see equation
1
, where
, is determined at the
N
nodes, see equation
1
, where ,
, and
and are node-dependent weights used to control the influence of energies for
a particular node,
n
, at different stages of the deformation.
are node-dependent weights used to control the influence of energies for
a particular node,
n
, at different stages of the deformation.
Mesh deformation uses a `greedy' algorithm which is similar to that presented in [ 11 ]. However, we introduce a specific stage, known as relaxation, that controls the problems of self-intersection and leakage. The mesh is refined, that is more nodes are added, using a coarse to fine strategy, such that the minimum number of nodes are used to represent the given shape. Thus, the deformation process involves automatically initialising the mesh in the feature object and then iteratively ballooning, relaxing and refining the mesh until convergence.
The internal energy,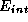 , aims to prevent self-intersection of the mesh surface by enforcing
tension and rigidity, see figure
2
a. The scale-invariant energy for node
n
is calculated using its neighbours, the set of nodes
, aims to prevent self-intersection of the mesh surface by enforcing
tension and rigidity, see figure
2
a. The scale-invariant energy for node
n
is calculated using its neighbours, the set of nodes and their centroid
and their centroid .
.

Where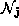 is the position vector of the
is the position vector of the node in the set
node in the set . The internal energy, see equation
2
gives an indication of the smoothness at that point in the model and is
similar to the topological constraint reported in [
8
]. It is the ratio of the distance of node
n
from
. The internal energy, see equation
2
gives an indication of the smoothness at that point in the model and is
similar to the topological constraint reported in [
8
]. It is the ratio of the distance of node
n
from to the mean distance of the nodes in
to the mean distance of the nodes in from
from .
.
Where is the internal energy and
is the internal energy and is the position vector at node
n
. In minimising the internal energy, node
n
can move towards the centroid of its neighbouring nodes or
alternatively, the neighbouring nodes can move away from each other
increasing the mean distance of the nodes in
is the position vector at node
n
. In minimising the internal energy, node
n
can move towards the centroid of its neighbouring nodes or
alternatively, the neighbouring nodes can move away from each other
increasing the mean distance of the nodes in from
from . A change in the internal energy of a node effects the internal
energies of all neighbouring nodes.
. A change in the internal energy of a node effects the internal
energies of all neighbouring nodes.
The image energy seeks to distinguish the object feature from the rest of the image with a numerical value. Often this is based on the edges found using an edge detection algorithm [ 4 ], however, applying such an algorithm to this data produces strong noise edges and very weak or non-existent edges at the condyles because of the subtle change in greyscale intensities identifying the boundary. It has proved very difficult to produce an accurate model of the femur with gradient information.
As a novel alternative we use probabilistic labelling to drive the deformation process. Each voxel in the image is labelled with a likelihood that the voxel is bone based on its greyscale intensity, by modelling the volume histogram as the sum of two Gaussians. The first Gaussian seeks to imitate the distribution of intensities produced by the anatomy, such as compact bone and muscle, which emits a darker intensity. The second Gaussian denotes the lighter intensity producing anatomy, such as spongy bone and fat. These two categories are sufficient to distinguish the bone outline and as such, for simplicity, distributions will be denoted as the bone and nonbone Gaussians, despite the bone Gaussian encompassing fat.
Frank
et al.
[
5
] describe a method of modelling simultaneously three tissue types by
fitting Gaussian distributions to a brain volume histogram using the
Marquardt-Levenberg minimisation algorithm [
9
]. We modify this technique for modelling the
bone
and
nonbone
Gaussians, as illustrated in figure
2
b. Thus we obtain functions
bone
and
nonbone
defined at each intensity
v
with constants ,
, ,
, ,
, ,
, and
and , derived from the minimisation.
, derived from the minimisation.
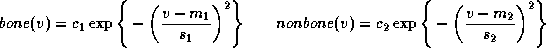
The probability of bone at each voxel in the volume with intensity v can then be generated with:
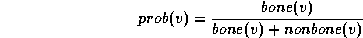
This probability is converted into an image energy value using an exponential function as shown in figure 2 c. We require high probabilities that indicate definitely bone to have a low energy and low probabilities, a very high energy. Probabilities up to 0.5 are likely to denote bone and as such should also have a low energy but past this level we want discouragingly high energies. The exponential function can be used to model this with constants A and B , see equation 3 .
The inflation energy,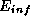 , is derived from a distance transform acquired from the probabilities
of bone and non-bone discussed above. The use of the word inflation to
describe the mechanism of the distance transform relates to the
ballooning of the mesh from within the object boundary, as opposed to
deflating a mesh onto an object. The distance from each voxel to the
nearest presumed femur boundary is calculated in order that a ballooning
energy can move nodes to feature boundaries. A feature boundary occurs
when the probability of bone falls from >0.5 to some lower likelihood. A
Chamfer filter is passed over the image to label voxels with an integer
approximation to their distance from the nearest surface point, see [
3
,
2
].
, is derived from a distance transform acquired from the probabilities
of bone and non-bone discussed above. The use of the word inflation to
describe the mechanism of the distance transform relates to the
ballooning of the mesh from within the object boundary, as opposed to
deflating a mesh onto an object. The distance from each voxel to the
nearest presumed femur boundary is calculated in order that a ballooning
energy can move nodes to feature boundaries. A feature boundary occurs
when the probability of bone falls from >0.5 to some lower likelihood. A
Chamfer filter is passed over the image to label voxels with an integer
approximation to their distance from the nearest surface point, see [
3
,
2
].
The original mesh is icosahedron shaped with 12 nodes and 20 faces. This shape approximates a sphere which has low curvature but with few nodes. The placement of the mesh in the volume can be achieved automatically and reliably by identifying the distinctive rings of compact bone that occur at the stem of the femur. Each node is likely to be some way from the object surface and using only a few nodes in the initial mesh will prevent considerable initial self-intersection.
The process of ballooning is the primary means of deforming the mesh to the feature boundary and is succeeded by the stages of relaxation and refinement. Ballooning, relaxation and refinement iterates until the mesh has reached a total cost convergence and all face edges are shorter than the minimum length, see section 3.7 , such that no more refinement will occur. During ballooning the nodes are deformed in a normal direction to the mesh surface under the influence of the inflation energy which dominates the other energies.
The weights for each energy at node
n
were determined to be empirically ,
, and
and where
e
is the value of the inflation energy at node
n
. The internal energy weight is related to the inflation energy, such
that the smoothness of the mesh is more important towards the object
boundary which is also when the image energy asserts its influence on
the total cost.
where
e
is the value of the inflation energy at node
n
. The internal energy weight is related to the inflation energy, such
that the smoothness of the mesh is more important towards the object
boundary which is also when the image energy asserts its influence on
the total cost.
Allowing a less smooth surface at areas far from the object boundary is necessary to facilitate tube like movement of the mesh from the stem of the femur to the condyles. However, this can lead to problems of self-intersection [ 8 ], as the model has no means of knowing if it is self-intersecting globally. A failure to acknowledge the problem leads quickly to an unintelligible, tangled mesh.
Nodes can also become trapped in local minima caused by noise. The inflation energy does not take account of whether the boundary it drives the mesh to is noise or actually the feature. Hence, the amount of high energy created by the noise can be unsurmountable, especially if the internal energy never becomes excessively high because of mesh refinement, and the node remains trapped.
In order, to deal with the problems of self-intersection, local minima and leakage, as shown in figure 3 , another stage is required in the deformation process, this is known as relaxation.
Relaxation serves three purposes, preventing self-intersection, shifting nodes out of local minima and preventing leakage. The inflation energy, or the pulling force to the object boundary, is removed completely so that the mesh is affected by its own smoothness constraints and the probabilistic labelling. The justification for this is that the inflation energy can not differentiate image feature from noise and is merely used by the model as a guide to the feature boundary.
The first phase of relaxation sets the weights to ,
, and
and . The nodes are permitted to move in any direction to achieve greater
smoothness, but are restrained from transversing the object boundary by
the image energy. The end result is nodes are repositioned to a position
such that the mesh is smoother, lowering the internal energy which has
been permitted to reach high levels due to the inflation energy and
reducing the likelihood of the surface self-intersecting. A convenient
side effect allows nodes lodged in local minima to spring out, because
the inflation energy, which has prevented movement, is removed and the
internal energy has built up sufficiently to overcome any high image
energy.
. The nodes are permitted to move in any direction to achieve greater
smoothness, but are restrained from transversing the object boundary by
the image energy. The end result is nodes are repositioned to a position
such that the mesh is smoother, lowering the internal energy which has
been permitted to reach high levels due to the inflation energy and
reducing the likelihood of the surface self-intersecting. A convenient
side effect allows nodes lodged in local minima to spring out, because
the inflation energy, which has prevented movement, is removed and the
internal energy has built up sufficiently to overcome any high image
energy.
The second phase of relaxation involves only nodes that meet a
particular criterion that implies the node is outside the object
boundary and leaking. The weights ,
, and
and are used. Leakage occurs when nodes are added, during refinement, to
areas outside the feature boundary and thus become trapped behind a high
wall of image energy; or the node escapes the feature boundary because
of edge discontinuities and subsequently becomes lodged in a local
minimum outside the boundary. If the positions of these nodes are not
changed, the mesh begins to grow out causing gross malformations.
are used. Leakage occurs when nodes are added, during refinement, to
areas outside the feature boundary and thus become trapped behind a high
wall of image energy; or the node escapes the feature boundary because
of edge discontinuities and subsequently becomes lodged in a local
minimum outside the boundary. If the positions of these nodes are not
changed, the mesh begins to grow out causing gross malformations.
We now search for nodes that would prefer to move in a negative normal direction to the surface of the mesh but are prevented from doing so by a high image energy, the characteristic predicament of a node positioned outside the object boundary. These nodes are then retracted to create a smoother leak-free mesh using the node's internal energy and ignoring its image energy.
Adding new nodes to the mesh is vital for producing a surface which embodies the detail of the object feature, known as refining. We require a `minimum length' for a face edge which is the shortest length of a face edge that we are permitted to refine. This minimum length determines the coarseness of the final femur mesh and is derived from the width of the femur stem, see section 3.4 .
The surface is refined using a coarse to fine strategy when all nodes for the current mesh are in a stable position, i. e. convergence. Face edges longer than twice the minimum are sought; if no edges meet this criteria the length is reduced by a given amount and so on until some edges are refined. The new node is placed at the midpoint of the nodes at either end of the edge being refined, see [ 10 ].



N Hill