The spatial correlation estimator
[3]
involves estimation of the fractal dimension direct from equation (1)
. Each possible pair of pixels in (x,y) may be considered a sample dI =
| I(x
1
,y
2
)-I(x
2
,y
2
) | and dp=sqrt((x
1
-x
2
)
2
+(y
1
-y
2
)
2
). The gradient of a linear fit to the data { log(dI), dp} will be H and
the fractal dimension given by D=3-H. In our implementation of this
approach we do not average |dI| over pixel pairs with the same nearest
integer separation - a method used in
[3]
to reduce computational expense.
Voss has shown
[12]
that a two-dimensional FBM surface, I(x,y), has a Fourier power spectrum
F(f,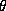
) proportional to f
-(b+1)
, where b=2H+1. We may therefore calculate b, and hence H and D, from a
linear fit to the data { log(F(f,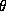
)), log(f) }. We refer to this method as the Fourier estimator
[4]
.
We also assess two variants of this method. Firstly, the tapered Fourier estimator in which the Fourier spectrum is obtained by averaging the Fourier spectra of tapered sub-windows of the image sample - this approach eliminates the possibility of the estimate being shifted by high frequency terms introduced by the periodicity assumption of the Fourier transform. Secondly, the ring Fourier estimator in which the two-dimensional power spectrum is collapsed down into a single dimension by taking the mean power over `rings' consisting of coefficients with same frequency when rounded to the nearest integer; computational expense is reduced by performing the linear fit over substantially fewer points.
If a set in 3-D space is statistically self-similar, then the number of
boxes of size (L x L x L) needed to cover the set obeys the power law
N(L)
L
-D
, where D is the fractal dimension.
Each pixel in a texture may be considered to be a point in 3-D space (intensity forming the third dimension). Assuming a self-similar fractal set the dimension D may be estimated from the slope of a linear fit to the data { log L, -log(N(L)) }, having calculated N(L) for several L. This is the box counting estimator [6] [5] . In [5] pixel intensity was effectively scaled to the same range as pixel co-ordinates prior to estimation.
The method does not assume a continuity between samples (unlike the following surface based methods) and it is valid only at large box sizes for which the discrete I(x,y) more closely approximates a continuous signal. We calculate the minimum box size to be used as
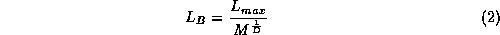
where M is the number of points in the set (pixels) and L_max is the box size which encloses the entire set. This limit was proposed as a guideline in [6] .
Each pixel in a texture image may be considered to be a cuboid with length and width equal to the pixel dimensions, and height equal to pixel intensity, so forming a set of adjacent `skyscrapers'. The total exposed surface of these skyscrapers forms a measure of the surface area of the texture. The area may be calculated at different integer ruler sizes, L, by averaging adjacent pixels to generate a new image with pixel size L. Assuming the texture is a continuous self-similar fractal then surface area and ruler size follow the relation
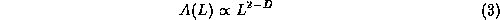
The fractal dimension, D, may be inferred from the slope of { log(A(L)), log (L) }. We refer to this as the surface estimator [7] .
Consider each pixel in the texture to be a point in discrete 3-D space, again using integer pixel intensity as the third dimension. Let M(L) be the number of points in the set obtained by dilation of the texture set using a spherical operator of size L, (i.e. all points in the discrete space which are within a distance L of a member of the texture set are added to the set). The change in surface area of the texture at a ruler size of L is obtained as
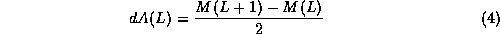
It is assumed
[9]
that equation (3)
is valid for dA(L) as it is for A(L), and the fractal dimension may be
inferred from the slope of { log(dA(L)), log(L) }. The method is known
as the blanket estimator
[9]
.
In [9] it is stated that use of dA(L) is equivalent to A(L) where the set accurately conforms to the fractal model. We suggest a modified blanket estimator in which
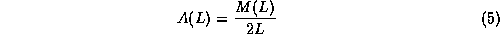
and we use equation (3)
to derive the fractal dimension from the slope of { log(A(L)), log(L) }.