The information associated with a labelling model can be encoded in two ways. Firstly, it can be encoded within a single labelling model rule tree which is capable of representing quite flexible layout and occurence constraints by using the SEQ, AGG, ?SEQ, ?AGG, CHO and ACC operators. Secondly, it can be encoded within a forest of (individually) far more constrained rule trees which only use the SEQ operator and look exactly like layout models, except for the fact that they have a label associated with each of their vertices.
We call the process of taking a single labelling model rule tree and generating an equivalent forest of (SEQ-only) rule trees resolving a rule tree. This is analogous to using a grammar generatively to facilitate recognition by synthesis approaches to linguistic analysis.
It should now be clear that performing labelling using rule trees is conceptually very straightforward. Firstly, we resolve the labelling model to produce a forest of rule trees. Secondly, we take each of the trees in turn and attempt to match it against the layout model, vertex by vertex. The set of valid labelling hypotheses is simply given by the matched rule trees (if any).
The approach to labelling described above is appealing, but its
computational feasibility depends on the number of alternatives
generated by each labelling operator applied at each vertex of the
labelling model. For any vertex within a rule tree, this depends only on
two things: the type of the current vertex; and, the number of
alternatives for each child of the current vertex. Thus the overall
complexity of the computation can be specified recursively by defining
the complexity
I
at a node (
v
) in terms of
, the value of
I
at the
i
'th child of vertex
v
.
If vertex
v
has
n
children, then we may calculate
I
for vertex
v
as follows:
How we calculate
I
for a vertex.
Vertex type
Formula
Vertex type
Formula
Form
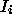
Word
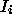
Character
1
SEQ
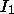
AGG
?SEQ
?AGG
CHO
ACC
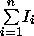
Unfortunately, it is easy to show that the value of
I
calculated at the root vertex of practical labelling models is typically
of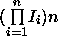
in size, where
c
is the number of characters within each hand-printed word;
w
is the number of words; and,
p
is the number of different layout possibilities for the words. However,
we have developed a far more computationally efficient approach which
reduces computational requirements to approximately
whilst guaranteeing to find all of the valid labelling hypotheses.
A particularly attractive feature of rule trees is that they allow us easily to gather statistical information concerning the constraining properties of a labelling model. For example, given any labelling model, we can define the maximum number of valid labellings that will be found (call this A ) without reference to any particular layout model. We can also, if desired, calculate a refined (potentially lower) value for A based on a given layout model, or calculate statistics concerning the mean value of A , etc.
A C++ class library implements the functionality of rule-trees by allowing the instantiation of various specialisations of an abstract base class called ``node''. For example, an object of type ``seq_node'' imposes the constraints associated with a SEQuence vertex. Each node object maintains an ordered list of its children, and member functions are available to alter the contents of this list, thus rule trees are created in a top-down fashion, starting from the root vertex.
A high level graphical user interface has also been produced which enables trees to be edited graphically. The GUI allows the definition of any tree to be written to a file and reloaded at a later date, thus it is possible to define and store a set of different labelling or layout models without resorting to knowledge or use of the class library. Both the class library and the GUI are integrated within TABS [ 1 ] (a rapid development-oriented software framework).
Cracknell C R W