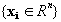 , where correspondence is established between the values at each index
of
, where correspondence is established between the values at each index
of , then each vector can be rewritten:
, then each vector can be rewritten:
3D Point Distribution Models of the Cortical Sulci
A. Caunce & C.J. Taylor
Dept. Medical Biophysics, University of Manchester,
Oxford Road, Manchester. M13 9PT.
ac@sv1.smb.man.ac.uk
Abstract
In this paper we present the first steps in the development of a statistical shape model, specifically a point distribution model (PDM), of the cortical surface of the brain. This will ultimately be used to locate, label, and describe the cortex, for visualisation, diagnosis, and quantification. In order to produce the model it was necessary to find and label the sulcal fissures on a series of MR images. Due to the complexity of the surface, an automated method was developed to facilitate development of a full surface model. Automating the marking process introduced the problem of identifying correspondences between examples, the knowledge of which is essential to the development of a PDM. Various methods were investigated to solve this problem including simple point matching and more complex curve matching. Each is outlined and discussed. The models obtained so far provide interesting insights into the shape and cortical pattern variations over a group of normal subjects.
1 Introduction
Many diseases of the brain, including schizophrenia and Alzheimer’s, are accompanied by structural, functional, and volumetric changes, both from the normal condition and over time. The aim of the work presented here is to develop a shape model of the cortex, specifically a Point Distribution Model (PDM) [6], which can incorporate knowledge of these changes and can aid in the automated interpretation of 3D head images by locating cortical landmarks in new examples. The model may be used not only in visualisation of the segmented structure, but also in detection of abnormality, monitoring the progress of a disease, and comparing characteristics within and between groups. The latter could aid in the diagnosis of a new patient by ascertaining the group model which best fits the subject. In addition the model can provide a means by which new examples can be co-registered for direct structural and functional comparisons.
Various approaches have already been used to segment 3D head images. Some authors use clustering techniques, which tend to be more effective with multi-sequence data[4][10], others have used image morphology [5][17]. However, although useful for visualisation of gross structure, the results of such methods provide no information about the location of particular areas. In general, the location and measurement of specific areas has required an expert user to label them manually [14][21]. In order to extract and label structures automatically the information must be incorporated into the model used. Several such anatomical atlases have been developed [19], but these tend to be developed from as little as one subject brain. Such atlases usually deform to the new example using intensity information or a combination of prescribed transformations [1][8], sometimes user driven [9]. These take little or no account of the natural variation of the subject and its possible configurations, the resulting labelling may therefore be unreliable. In contrast Hill et al. [11] developed a 3D PDM of structures in the head from a training set of examples which allowed knowledge of anatomical variation to be used when searching. However, the structures chosen were considerably simpler than the cortical surface, which meant that manual point correspondence was possible. Also the model was developed on a slice by slice basis and therefore takes no account of head rotation in 2 directions. Subsol et al. [23] developed a fully 3D model of skull ridges from a set of example CT scans. The ridges were detected and matched automatically to produce an atlas but, despite this, the authors still chose to model its variation using mathematical modal analysis based on physical structure [15] rather than statistical observation.
The work presented here is fully 3D and aims not only to extract the cortical surface in new MR images of the head, but to simultaneously label major landmarks, like the sulcal fissures, which are generally used as anatomical reference points [18] and as a diagnostic aid [21]. Sandor & Leahy [20] developed a model which could locate and label a small number of sulci, but again the model had no built in knowledge of their structural variations and configurations. To incorporate such knowledge into a shape model they need to be identified on every example and corresponded between examples. This poses a problem since the surface fissuring is complex in terms not only of density, but also configuration [16]. Most sulci exhibit breaking and branching, and can be duplicated in some individuals, and absent in others. It was necessary therefore to develop some way of automating the process. The first stage, that of locating the sulci, was achieved using some simple morphological processing to automatically place points over the mouths of the fissures on 3D MR images Szekely et al. [24] used a similar technique, except by working with the whole image instead of the hull they obtained points which were some distance above the cortical surface. The second stage, that of corresponding the points between sets was approached using seven different methods which are presented and compared here. The majority of these have been developed to tackle, specifically, the problems peculiar to the complex configuration of the cortex. All the methods are based on an iterative approach inspired by the work of Besl and McKay [3] and Zhang [25], and several are an extension of the curve matching idea presented by Subsol et al. [22]. Quantitative criteria were used to compare the quality of the models developed from each method. The most satisfactory has been used to identify and visualise major sources of variation between normal individuals.
2 Point Distribution Models
PDMs have been used to model many classes of variable objects ranging from faces [13] to electrical components [7]. Full details of the PDM can be found in [6] but the following gives a brief description.
Given a set of example pattern vectors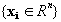 , where correspondence is established between the values at each index
of
, where correspondence is established between the values at each index
of , then each vector can be rewritten:
, then each vector can be rewritten:
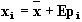 (1)
(1)
where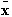 is the mean pattern vector,
E
is the matrix whose columns are the eigenvectors of the co-variance
matrix of the set, and
is the mean pattern vector,
E
is the matrix whose columns are the eigenvectors of the co-variance
matrix of the set, and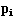 is an n-dim vector of parameters describing the degree to which
is an n-dim vector of parameters describing the degree to which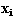 varies from
varies from in a way described by the corresponding eigenvectors. Each eigenvector
describes the way in which linearly correlated
x
ij
move together over the set, referred to as a 'mode of variation'. New
examples, not included in the training set, can be generated by
manipulating the elements of
p
. To model objects in three-dimensions the
in a way described by the corresponding eigenvectors. Each eigenvector
describes the way in which linearly correlated
x
ij
move together over the set, referred to as a 'mode of variation'. New
examples, not included in the training set, can be generated by
manipulating the elements of
p
. To model objects in three-dimensions the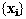 are constructed using the co-ordinates of descriptive features of each
example. The features must correspond to the same 'points' on each
object. Given co-ordinates
are constructed using the co-ordinates of descriptive features of each
example. The features must correspond to the same 'points' on each
object. Given co-ordinates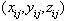 at each feature j of object i, the shape vector is:
at each feature j of object i, the shape vector is:
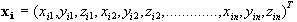
Appropriate features may be corners, edges, borders, surface patterns, etc. These can often be identified and corresponded by hand, but for extremely complex subjects, like the cortical surface, an automated approach preferable.
3 Automatic Location of the Sulci
The complex characteristics of the cortex provide a sizeable obstacle in the development of a PDM, where identical features must be labelled and corresponded in each example. An early attempt was made to build a small model of a portion of the cortex, placing points over the sulcal fissures by hand in 3D Magnetic Resonance images. The results indicated that such a model was viable but the matching process was extremely difficult and time-consuming. Therefore a method was developed to automatically locate the sulcal fissures for use in a model. All images used were T1 weighted with non-cubic voxels of 1 x 1 x 1.5 mm, and approximately 60 slices each. All had some upper slices missing. The new method capitalised on the high contrast in the images between the grey matter and the cerebro-spinal fluid (CSF). Each image was pre-processed by hand to remove the ‘skull’ and then thresholded. A closing operation was used to produce an approximation to the convex hull of the brain in a similar way to that of Sandor & Leahy [20]. The original (segmented) image was subtracted from the hull leaving a representation of the sulcal fissures. This was intersected with the surface of the hull to leave a collection of ribbons representing the mouths of the sulci. Finally these ribbons were thinned to give a set of lines following the medial axes of the sulci. These were converted to points at the intersection of each slice. Figure 1 illustrates this process. Due to the variation between subjects this generated point sets with numbers of points varying between 4000 and 6000 over 16 examples. No feature correspondences were established between points.
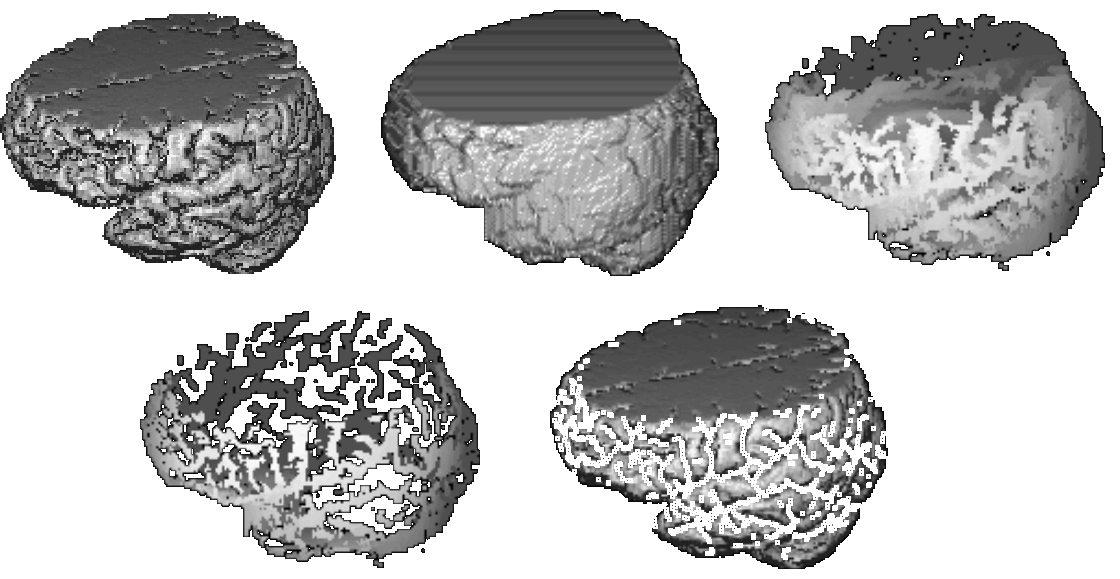
Figure 1. Left to right, top to bottom: segmented brain, hull, subtraction image (sulci), intersection with hull surface, thinned point set superimposed on the brain.
4 Establishing Point Correspondences
Having automatically obtained a set of points following the sulci on each example in the training set, it was necessary to correspond the points between examples to build a PDM. The problem actually breaks down into two interdependent parts: set alignment and point matching. Both are tackled simultaneously by the Iterative Closest Point algorithm (ICP) [3][25]. Using this algorithm as a basis, several methods were developed to correspond the point sets generated using the method from section 3.
Method 1. The sparsest point set was chosen as the ‘master’. Each of the others was matched to it using the ICP algorithm. Closest points were established using Euclidean distance and aligned using the quaternion method [12]. A user-defined threshold was applied to exclude matches over a certain distance apart. This eliminated the effect of outlying points including possible distortions caused by different numbers of slices present. Matching was considered complete when the change in pose of the new point set was sufficiently small. At this stage all matches to any one point in the master set, in either direction, were combined to form an average matched point. Therefore no information was lost from the new point set but the final correspondents were not necessarily actual points. Using a contrived example, Figure 2 shows the closest points obtained, in one direction.
This basic approach takes no account of connectivity. Although the point sets are sparse they follow the lines of the sulci and this information can be used to improve the accuracy of the match. A method was required which attempted to ensure that neighbouring points on one sulcus were attracted to neighbours on another. Each of the following methods relies on initially identifying and labelling the curve segments in each point set. Also, the user defined threshold was too arbitrary so a more principled statistical approach was employed by examining the distribution of distances at each iteration. The threshold was expressed as a number of standard deviations allowed from the mean before exclusion. The fully automated method employed by Zhang [25] was not adopted because the assumptions of only small shape differences do not hold.
Method 2. After closest points were established at each iteration of the ICP, votes were cast to establish curve matches. The largest number of points on a curve matching to one other established the match. Subsol et al. [22] applied a similar technique although they employed a threshold to establish correspondence. The points were then re-matched to their closest neighbour on the matching curve only. Figure 3 indicates the correspondences obtained.
As well as connectivity information the point sets actually contain more clues as to the identity of each sulcus. For example, if sulci are assumed to be in approximately the same position on each example, and of approximately the same length (including breaks), then surface normals should be similar at corresponding points. Also the surface orientation of a particular sulcus tends to be the same on each subject.
Method 3. In order to further restrict the points which were allowed to match more attributes were added into the distance measure. The surface normals at each point were used, which reduced scope, and the principle axis of the curve containing the point, which ensured curves running in similar directions were more attracted to each other. Barequet & Sharir [2] referred to this type of descriptive attribute as directed footprints and used them to generate candidate transformations in their one pass alignment method. So for point j on image i and point l on image k the new distance measure used was:
 (3)
(3)
where
 are the principle axes of the curves containing points j and l. Figure 2
shows the closest points obtained using this distance measure. (The
curve matching gives the same point correspondences as method 2 for the
particular example shown).
are the principle axes of the curves containing points j and l. Figure 2
shows the closest points obtained using this distance measure. (The
curve matching gives the same point correspondences as method 2 for the
particular example shown).
|
|
|
|
|
|
|
|
|
|||||||||
|
Figure 2. Closest points |
Figure 3. Final point correspondences after curve matching. |
|||||||||||||||
Method 4. After a curve match was established, orientation and location differences often caused the point correspondences to be clustered around one portion of the curve. To counteract this the matched curve segments were aligned using their centres of gravity (COG), and then scaled before points were matched. Figure 4 illustrates the process and Figure 3 shows the final correspondences.

Figure 4. Matched curves are aligned and scaled before points are corresponded.
Finally, it is important that fragments of one sulcus are attracted to fragments of one other, and that multiple instances of one sulcus are attracted to their single counterpart This led to the development of two more methods.
Method 5. To combat severe fragmentation and allow multiple curves to match to each other a correspondence chain was used to establish small subsets of curves allowed to match. Firstly a one-to-one correspondence was found, say between curve j on image i and curve l on image k. Any curves on image i which also matched curve l were added to the set for i. Similarly any curves on k which matched j were added for k. This process was repeated for the new curves added until no more matches were found. The established sub-sets were then aligned, as in method 4, before point matching. Figure 3 shows the correspondences in one direction.
Method 6. Method 5 was tested without the alignment of the sub-sets before matching. Figure 3 shows the final point correspondences.
5 Results
Each method from section 4 was used to correspond 16 point sets, with numbers of points between 4000 and 6000, automatically extracted from 3D MR images. All of the methods took several hours to complete but method 1 was by far the fastest. All of the methods produced a plausible mean shape but when the modes of variation were inspected through animation, some showed more coherence than others. Intuitively, it might be expected that the better model would exhibit more consistency, so that points of one curve would ‘stick together’ when the model was animated. Two tests were devised to assess the models.
Firstly, a target set of points was generated from a new image, using the method outlined in section 3. The model was forced to fit to this target set using an ICP-type algorithm. The closest point was found on the target for each model point, then a fit was made and the process was repeated. After 10 iterations the mean, max., and SD of the point distances were measured, and the results are given in Table 1. This method assesses the ability of the model to adopt the shape of the target but does not assess its accuracy as a model or its efficiency in search.
|
Method |
Mean |
Max. |
SD |
|
1 |
2.82962 |
8.60524 |
1.41289 |
|
2 |
2.69898 |
9.16754 |
1.38196 |
|
3 |
2.65864 |
8.26094 |
1.32282 |
|
4 |
2.67766 |
8.61014 |
1.34267 |
|
5 |
2.71017 |
8.48377 |
1.38364 |
|
6 |
2.64055 |
7.96908 |
1.30309 |
Table 1. Model to target point distances.
Secondly, to measure coherence, a value was calculated for each mode k:
 (4)
(4)
where
N
is the total number of points in the model,
n
i
is the number of points in the spherical neighbourhood of point i, and
the unit vectors are the displacement directions of the points.
are the displacement directions of the points.
Figures 5 & 6 show the results for each method over all modes using two different neighbourhood sizes, the smaller being engineered to include only immediate neighbours. Notice that method 5 performs best over all the modes. It is interesting that different modes represent different ‘diversities of movement’ and that a pattern has emerged which is repeated over all the models, although actually, no assumptions can be made about the relationship of one mode to another.
|
|
|
|
Figure 5. |
Figure 6. |
To examine the models a series of static displays were developed as follows.
Figure 7 shows all four displays of the lateral view of mode 1 obtained from method 5 above. The pattern view (bottom left) shows the independent movement of at least one of the sulci, and the shape view (top right) shows two distinct areas of common movement. Figure 8 shows the same shape view from above which indicating that mode 1 represents a shape change which may be interpreted as torque of the brain.
|
|
|
|
Figure 7. Left to Right, top to bottom: Global co-ordinates, normal movement (shape), surface movement (pattern), local co-ordinates. |
Figure 8. Top view of shape display. Torque.
|
The following Figures show some of the more interesting details to emerge over the modes obtained.

Figure 10. The shape view of mode 2 (left and centre) shows a change in size of the frontal lobes, and the pattern view (right) again shows independently moving structures.
|
|
|
|
Figure 11. Mode 3 models a striking shape change in only one temporal lobe.
|
Figure 12. Mode 4 (pattern view) clearly shows the emergence of several sulci moving together at the anterior end. |
6 Discussion
From Table 1 and Figures 5 & 6 it is clear that method 1 (basic ICP) produces the worst results, as might be expected. No attempt has been made to keep neighbours together by matching curve segments. Doing this (method 2) immediately improves results, and adding meaningful attributes to the distance measure (method 3) considerably improves the model. The most contradictory result is that of method 5. This method attempts to handle the complex structures of the cortical sulci and shows by far the best coherence over all the modes, yet it gives one of the poorer matches to the target. Perhaps one is a direct result of the other. The constraints placed on the model for neighbours to ‘stick together’ prevents it from adopting a new and complex shape. It might be conjectured that a model constructed from many more examples would be able to adopt such a shape without having to sacrifice consistency. Figures 7-12 illustrate the coherence of method 5 and show that meaningful results are emerging from the model.
References
[1] Bajcsy, R. and S. Kovacic, Multiresolution Elastic Matching. Computer Vision, Graphics, and Image Processing, 1989. 46: p. 1-21.
[2] Barequet, G. and Sharir, M., Partial Surface Matching by Using Directed Footprints . Ann. ACM Symp. on Computational Geometry, Philadelphia, PA, 1996. p. C9-10.
[3] Besl, P.J. and McKay, N.D., A Method for Registration of 3-D Shapes. IEEE Trans. PAMI, 1992.14(2): p. 239-256.
[4] Bezdek, J.C., L.O. Hall, and L.P. Clarke, Review of MR Image Segmentation Techniques Using Pattern Recognition. Medical Physics, 1993. 20(4): 1033-1048.
[5] Bomans, M., et al. , 3-D Segmentation of MR Images of the Head for 3-D Display. IEEE Trans. on Medical Imaging, 1990. 9(2): p. 177-183.
[6] Cootes, T.F., et al . Training Models of Shape from Sets of Examples . in BMVC . 1992. Springer-Verlag.
[7] Cootes, T.F., et al. , Active Shape Models - Their Training and Application. Computer Vision and Image Understanding, 1995. 61(1): p. 31-59.
[8] Gee, J.C., M. Revich, and R. Bajcsy, Elastically Deformaing 3D Atlas to Match Anatomical Barian Images. J. Comp Assist. Tomog., 1993. 17(2): p. 2250-236.
[9] Grietz, T., et al. , A Computerised Brain Atlas: Construction, Anatomical Content, and Some Applications. J. Comp. Assist. Tomog., 1991. 15(1): 26-38.
[10] Hall, L., et al. , A Comparison of Neural Network and Fuzzy Clustering Techniques in Segmenting Magnetic Resonance Images of the Brain. IEEE Trans. Neural Networks, 1992. 3(5): p. 672-682.
[11] Hill, A., et al., Model-Based Interpretation of 3D Medical Images . Proc. BMVC 1993.
[12] Horn, B.K.P., Closed-form solution of absolute orientation using unit quaternions . J. Opt. Soc. Am. A, 1987. 4(4): p. 629-642.
[13] Lanitis, A., Taylor, C.J., and Cootes, T.F ., An Automatic Face Identification System Using Flexible Appearance Models , 1994, Proc. BMVC, York, UK. Vol. 1:p. 65-74.
[14] Loftus, W.C., Tramo, M.J., Gazzaniga, M.S., Coritcal Surface Modeling Reveals Gross Morphometric Correlates of Individual Differences , Human Brain Mapping, 1995, 3:p. 257-270.
[15] Nastar, C., Ayache, N., Frequency-Based Nonrigid Motion Analysis: Application to Four Dimensional Medical Images , IEEE Trans. Pattern Analysis and Machine Intelligence, 1996, 18(11):p. 1067-1079.
[16] Ono, M., S. Kubik, and C.D. Abernathy, Atlas of the Cerebral Sulci . 1990, New York: Georg Thieme Verlag.
[17] Orphanoudakis, S., G. Tzirita, and K. Haris, A Hybrid Algorithm for the Segmentation of 2D/3D Images . Information Processing in Medical Imaging, ed. Y.B.e. al. 1995, Netherlands: Kluwer Academic Publishers. 385-386.
[18] Rademacher, J., Galaburda, A.M., Kennedy, D.N., Filipek, P.A., and Caviness, Jr., V.S ., Human Cerebral Cortex: Localization, Parcellation, and Morphometry with Magnetic Resonance Imaging , J. of Cognitive Neuroscience, 4(4):p. 354-374.
[19] Roland, P.E. and K. Zilles, Brain Atlases - A New Research Tool. Trends in Neurosciences, 1994. 17(11): p. 458-467.
[20] Sandor, S. and R.M. Leahy, Towards Automated Labelling of the Cerebral Cortex Using a Deformable Atlas . Information Processing in Medical Imaging, ed. Y.e.a. Bizais. 1995, Netherlands: Kluwer Academic Publishers. 127-138.
[21] Sasodya, S., et al. , The Demonstration of Gyral Abnormalities in Patients with Cryptogenic Partial Epilepsy Using Three-Dimensional MRI. Arch. Neurology, 1996. 53: p. 28-34.
[22] Subsol, G., J.P. Thirion, and N. Ayache, First Steps Towards Automatic Building of Anatomical Atlases . 1994, INRIA: Tech. Rep. 2216.
[23] Subsol, G., Thirion, J-P., Ayache, N ., A General Scheme for Automatically Building 3D Morphometric Anatomical Atlases: Application to a Skull Atlas , 1995, INRIA: Tech. Rep. 2586.
[24] Szekely, G., et al., Mapping the human cerebral cortex using 3D medial manifolds. Visualisation in Biomedical Computing, 1992, SPIE 1808: p. 130-144.
[25] Zhang, Z., On Local Matching of Free-Form Curves. Proc. BMVC, 1992. p. 347-356.