


Next:
2 Background
Up:
A Method of
Previous:
A Method of
In this paper, we describe a method of pair-wise correspondence which
may be used for the automated landmarking of a class of shapes in 3D.
These landmarked shapes constitute a set of training examples which may
be used to construct a flexible template model of the shape. The model
we wish to construct is known as a Point Distribution Model (PDM) [
3
]. Such a model may be combined with statistical models of the greyscale
appearance of the modelled shape within training images to produce an
Active Shape Model (ASM) [
4
]. ASMs have been shown to perform accurately and robustly in the
segmentation of medical images in 2D [
13
] and 3D [
8
].
Currently, the construction of PDMs involves the manual identification
of a set of
L
landmarks
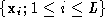 for each of
N
training examples of shape. A landmark is a point which identifies a
salient feature of the shape and which is present on every example of
the class. Manual definition of landmarks on 2D shape has proved to be
both time-consuming and subjective. The interactive identification of
landmarks in 3D images or on pre-segmented surfaces is considerably more
difficult and time-consuming than in the 2D case. These problems have
been the impetus behind some recent work on automated landmark
identification of 2D shape [
7
] and a partial extension of the method to 3D shape [
6
] which we use as the basis of the work described here.
for each of
N
training examples of shape. A landmark is a point which identifies a
salient feature of the shape and which is present on every example of
the class. Manual definition of landmarks on 2D shape has proved to be
both time-consuming and subjective. The interactive identification of
landmarks in 3D images or on pre-segmented surfaces is considerably more
difficult and time-consuming than in the 2D case. These problems have
been the impetus behind some recent work on automated landmark
identification of 2D shape [
7
] and a partial extension of the method to 3D shape [
6
] which we use as the basis of the work described here.
The framework for our method is the construction of a binary tree of
merged shapes. Once such a tree has been produced, a set of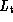 landmark points may be identified on the root (mean) shape of the tree
and the positions of these landmarks propagated out to the
landmark points may be identified on the root (mean) shape of the tree
and the positions of these landmarks propagated out to the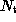 leaf (example) shapes. The algorithm used to construct this tree
requires a pair-wise corresponder which both matches shapes (so that
they can be merged) and measures the quality of the match (in order to
decide which pairs to merge).
leaf (example) shapes. The algorithm used to construct this tree
requires a pair-wise corresponder which both matches shapes (so that
they can be merged) and measures the quality of the match (in order to
decide which pairs to merge).
The pair-wise correspondence we seek is between two faceted
(triangulated) surfaces which represent examples from the same class of
object and a
non-rigid
transformation is required to map one surface onto the other. Here, we
present a novel method of pair-wise correspondence between 3D
triangulated surfaces. The algorithm locates a pair of matching
sparse
polyhedral approximations, one for each of the pair of surfaces by a
variant of the Iterative Closest Point (ICP) algorithm of Besl and McKay
[
2
]. Our development of this algorithm is symmetric and uses surface
normal information to guide the choice of point correspondences. Sparse
polyhedral approximations are produced by a triangle decimation. Once
pairs are matched, they are merged by computing the mean geometric
information of corresponded point pairs interpolated within locally
parameterised surface patches. These patches represent the triangles of
the sparse polyhedral approximation to the original shape surfaces.
We demonstrate the production of a densely triangulated mean shape from
a pair of smooth synthetic examples by the correspondence of their
sparse polyhedral approximations. We also present results of the use of
this pair-wise correspondence algorithm for the production of a binary
tree of merged shapes. In this case, for a complex biological shape -
the left ventricle of the brain.



Next:
2 Background
Up:
A Method of
Previous:
A Method of
Alan Brett
Wed Jul 9 16:24:02 BST 1997
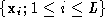 for each of
N
training examples of shape. A landmark is a point which identifies a
salient feature of the shape and which is present on every example of
the class. Manual definition of landmarks on 2D shape has proved to be
both time-consuming and subjective. The interactive identification of
landmarks in 3D images or on pre-segmented surfaces is considerably more
difficult and time-consuming than in the 2D case. These problems have
been the impetus behind some recent work on automated landmark
identification of 2D shape [
7
] and a partial extension of the method to 3D shape [
6
] which we use as the basis of the work described here.
for each of
N
training examples of shape. A landmark is a point which identifies a
salient feature of the shape and which is present on every example of
the class. Manual definition of landmarks on 2D shape has proved to be
both time-consuming and subjective. The interactive identification of
landmarks in 3D images or on pre-segmented surfaces is considerably more
difficult and time-consuming than in the 2D case. These problems have
been the impetus behind some recent work on automated landmark
identification of 2D shape [
7
] and a partial extension of the method to 3D shape [
6
] which we use as the basis of the work described here.


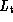 landmark points may be identified on the root (mean) shape of the tree
and the positions of these landmarks propagated out to the
landmark points may be identified on the root (mean) shape of the tree
and the positions of these landmarks propagated out to the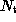 leaf (example) shapes. The algorithm used to construct this tree
requires a pair-wise corresponder which both matches shapes (so that
they can be merged) and measures the quality of the match (in order to
decide which pairs to merge).
leaf (example) shapes. The algorithm used to construct this tree
requires a pair-wise corresponder which both matches shapes (so that
they can be merged) and measures the quality of the match (in order to
decide which pairs to merge).