


Next:
5 Conclusions and Outlook
Up:
Needle Map Recovery
Previous:
3 The Robust Regularizer
The aim in this section is to explore the performance of the sigmoidal
regularizer compared to that of the conventional Horn and Brooks
algorithm. We start with comparison on noiseless, synthetic images, then
consider the degradation of needle-map recovery with increasing image
noise. Finally, we present a selection of real-world examples.
Our first test image is a Lambertian synthetic solid consisting of two
back-to-back segments of a sphere. At the line of symmetry where the two
segments meet, the tangent planes make an angle of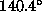 . This image was generated to test the relative ability of the two
schemes to recover the needle map of a piecewise-smooth object without
smoothing out the discontinuity where the two segments meet. The
resulting needle-maps and reconstructed images are shown in Figure 3. It
is clear that the sigmoidal regularizer yields a significant improvement
over the conventional Horn and Brooks algorithm, particularly in the
region of the centre-line.
. This image was generated to test the relative ability of the two
schemes to recover the needle map of a piecewise-smooth object without
smoothing out the discontinuity where the two segments meet. The
resulting needle-maps and reconstructed images are shown in Figure 3. It
is clear that the sigmoidal regularizer yields a significant improvement
over the conventional Horn and Brooks algorithm, particularly in the
region of the centre-line.

Figure 3:
Comparison of Horn and Brooks with Sigmoidal Regularizer algorithm on
synthetic image.
Part of the motivation for applying robust statistics to the
shape-from-shading problem is to improve noise rejection. To investigate
this, we use the same test image as previously, but with increasing
levels of additive Gaussian noise. Having shown in Figure 1 that the
sigmoidal regularizer yields better reconstruction results than Horn and
Brooks in noiseless conditions, Figures 4 illustrate that this advantage
is maintained on noisy images.

Figure 4:
Comparison of reconstructed images for 5% (top row) and 10% (bottom row)
added noise.
Figure 5 shows plots of normal error and ground-truth brightness error
for the two schemes. The normal error is the magnitude of the vector
difference between the recovered normal at a point, and the ground-truth
normal. The ground-truth brightness error is the difference between the
reconstructed image from noisy input and the
noiseless
test image of Figure 3.
In terms of normal error, the true measure of accurate needle-map
recovery, the sigmoidal regularizer demonstrates significant
improvements over the Horn and Brooks algorithm. Comparing the
reconstructed images against ground-truth, we also see that both
algorithms incorporate useful levels of noise rejection; the brightness
error measured against ground-truth rises more slowly than the
brightness error measured against the noisy input images, showing that
the schemes converge towards the underlying surface structure and do not
try to model noise artifacts. The sigmoidal regularizer demonstrates
excellent rejection of noise up to noise levels of 8-10%, i.e. Gaussian
noise of zero mean and unit variance with Signal-to-Noise Ratio of down
to around 10.
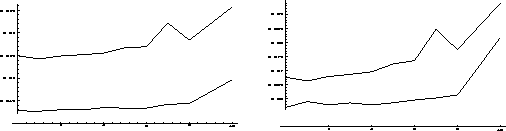
Figure 5:
Variation of normal error (left) and ground-truth brightness error
(right) with increasing image noise. In both cases, the top curve
corresponds to the Horn and Brooks algorithm, and the bottom curve is
due to the Sigmoidal regularizer.
Finally, to illustrate the effectiveness on real-world images, Figure 6
shows a noisy IndyCam image of a blu-tac model of a torus impaled on a
rod, together with the reconstructed images and recovered needle-maps
for the two algorithms. From left to right, the columns in Figure 6 show
the original image together with the reconstructed images obtained with
the Horn and Brooks algorithm, and the result produced using the
Sigmoidal regularizer. Shown below the reconstructed images are the
recovered needle-maps. The sigmoidal regularizer recovers a needle-map
containing finer curvature detail. Horn and Brooks's method invariably
oversmooths the sharp surface detail. In particular, the robust method
is much better at recovering the concavities and convexities of the
surfaces.
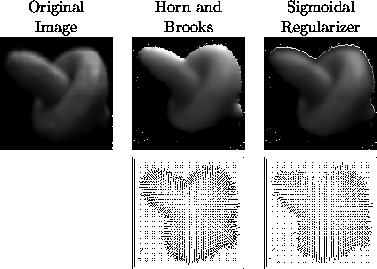
Figure 6:
Comparison of Horn and Brooks vs Sigmoidal Regularizer.



Next:
5 Conclusions and Outlook
Up:
Needle Map Recovery
Previous:
3 The Robust Regularizer
Benoit Huet
Tue Jul 8 11:31:38 BST 1997
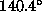 . This image was generated to test the relative ability of the two
schemes to recover the needle map of a piecewise-smooth object without
smoothing out the discontinuity where the two segments meet. The
resulting needle-maps and reconstructed images are shown in Figure 3. It
is clear that the sigmoidal regularizer yields a significant improvement
over the conventional Horn and Brooks algorithm, particularly in the
region of the centre-line.
. This image was generated to test the relative ability of the two
schemes to recover the needle map of a piecewise-smooth object without
smoothing out the discontinuity where the two segments meet. The
resulting needle-maps and reconstructed images are shown in Figure 3. It
is clear that the sigmoidal regularizer yields a significant improvement
over the conventional Horn and Brooks algorithm, particularly in the
region of the centre-line.





