


Next:
3 The Robust Regularizer
Up:
Needle Map Recovery
Previous:
1 Introduction
Central to shape-from-shading is the idea that local regions in an image
E
(
x
,
y
) correspond to illuminated patches of a piecewise continuous surface,
z
(
x
,
y
). The measured brightness
E
(
x
,
y
) will vary depending on the material properties of the surface (whether
matte or specular), the orientation of the surface at the co-ordinates (
x
,
y
), and the direction of illumination.
The
reflectance map
,
R
(
p
,
q
) characterises these properties, and provides an explicit connection
between the image and the surface orientation. The surface orientation
is characterised by the components of the surface gradient in the
x
and
y
direction, i.e.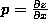 and
and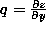 . The shape from shading problem is to recover the surface
z
(
x
,
y
) from the image
E
(
x
,
y
). As an intermediate step, we may attempt to recover a needle diagram,
describing the orientations of surface patches which locally approximate
z
(
x
,
y
).
. The shape from shading problem is to recover the surface
z
(
x
,
y
) from the image
E
(
x
,
y
). As an intermediate step, we may attempt to recover a needle diagram,
describing the orientations of surface patches which locally approximate
z
(
x
,
y
).
To simplify the problem, most research has concentrated on recovering
ideal Lambertian surfaces illuminated by a single point source located
at infinity [
2
]. A Lambertian surface has a matte appearance and reflects incident
light uniformly in all directions. Hence, the light reflected by a
surface patch in the direction of the viewer is simply proportional to
the orientation of the patch relative to the light source direction. If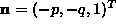 is the local unit surface normal, and
is the local unit surface normal, and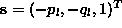 the global light source direction, then the reflectance function is
given by
the global light source direction, then the reflectance function is
given by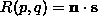 .
.
The image irradiance equation [
5
] states that the measured brightness of the image is proportional to
the radiance at the corresponding point on the surface, which is
R
(
p
,
q
). Normalising both image intensity and reflectance map, the constant of
proportionality becomes unity, and the image irradiance equation is
simply
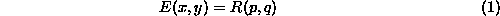
This equation succinctly describes the mapping between the
x
,
y
co-ordinate space of the image and the the
p
,
q
gradient-space of the surface, but provides insufficient constraints for
the unique recovery of the needle-map. Additional constraints, based on
assumptions about the structure of the recovered surface, must be
utilised. Invariably, it is smoothness of the needle-map that is
assumed. Hence, the goal is to recover the smoothest surface satisfying
the image irradiance equation. This is posed as a variational problem in
which a global error-functional is minimised through the iterative
adjustment of the needle map. Here we consider the formulation of Brooks
and Horn [
2
] which is couched in terms of unit surface normals. The error
functional is defined to be
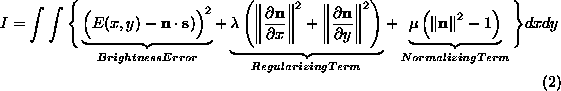
The functional has three distinct terms. Firstly, the brightness error
encourages data-closeness of the measured image intensity and the
reflectance function. It is the only term which directly exploits
shading information. The
regularizing term
imposes the smoothness constraint on the recovered surface normals; it
penalises large local changes in surface orientation, measured by the
magnitudes of the partial derivatives of the surface normals in the
x
and
y
directions. The final term imposes normalization constraints on the
recovered normals. The constants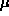 and
and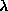 are Lagrangian multipliers.
are Lagrangian multipliers.
The functional is minimized by applying variational calculus and solving
the Euler equation:
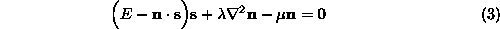
To obtain a numerical scheme for recovering the needle-map we must
discretise this variational equation to the pixel lattice by indexing
the surface normals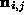 according to their co-ordinates (
i
,
j
) on the pixel-lattice. With this notation, the discrete numerical
approximation to the Laplacian is
according to their co-ordinates (
i
,
j
) on the pixel-lattice. With this notation, the discrete numerical
approximation to the Laplacian is
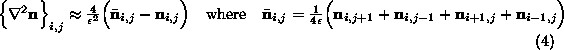
and is the spacing of pixel-sites on the lattice. Upon substitution, the
Euler equation becomes
is the spacing of pixel-sites on the lattice. Upon substitution, the
Euler equation becomes
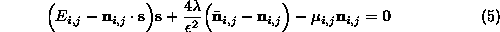
Rearranging this equation to isolate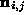 yields the following iterative scheme for updating the estimated normal
at the surface point corresponding to image pixel (
i
,
j
), at epoch
k
+1, using the estimate at epoch
k
:
yields the following iterative scheme for updating the estimated normal
at the surface point corresponding to image pixel (
i
,
j
), at epoch
k
+1, using the estimate at epoch
k
:
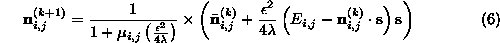
At first-sight, it appears necessary to solve for the Lagrangian
multiplier,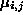 on a pixel-by-pixel basis. However, it is important to note that
on a pixel-by-pixel basis. However, it is important to note that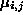 only enters the update equation as a multiplying factor which does not
effect the direction of update, so we can replace this factor by a
normalization step.
only enters the update equation as a multiplying factor which does not
effect the direction of update, so we can replace this factor by a
normalization step.



Next:
3 The Robust Regularizer
Up:
Needle Map Recovery
Previous:
1 Introduction
Benoit Huet
Tue Jul 8 11:31:38 BST 1997
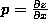 and
and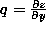 . The shape from shading problem is to recover the surface
z
(
x
,
y
) from the image
E
(
x
,
y
). As an intermediate step, we may attempt to recover a needle diagram,
describing the orientations of surface patches which locally approximate
z
(
x
,
y
).
. The shape from shading problem is to recover the surface
z
(
x
,
y
) from the image
E
(
x
,
y
). As an intermediate step, we may attempt to recover a needle diagram,
describing the orientations of surface patches which locally approximate
z
(
x
,
y
).


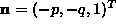 is the local unit surface normal, and
is the local unit surface normal, and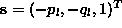 the global light source direction, then the reflectance function is
given by
the global light source direction, then the reflectance function is
given by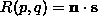 .
.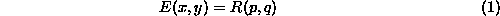
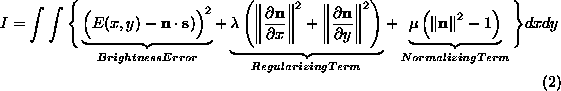
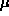 and
and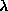 are Lagrangian multipliers.
are Lagrangian multipliers.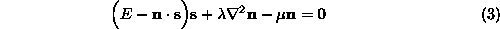
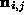 according to their co-ordinates (
i
,
j
) on the pixel-lattice. With this notation, the discrete numerical
approximation to the Laplacian is
according to their co-ordinates (
i
,
j
) on the pixel-lattice. With this notation, the discrete numerical
approximation to the Laplacian is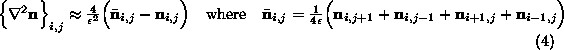
 is the spacing of pixel-sites on the lattice. Upon substitution, the
Euler equation becomes
is the spacing of pixel-sites on the lattice. Upon substitution, the
Euler equation becomes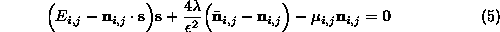
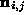 yields the following iterative scheme for updating the estimated normal
at the surface point corresponding to image pixel (
i
,
j
), at epoch
k
+1, using the estimate at epoch
k
:
yields the following iterative scheme for updating the estimated normal
at the surface point corresponding to image pixel (
i
,
j
), at epoch
k
+1, using the estimate at epoch
k
: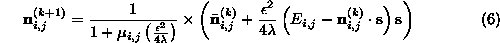
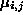 on a pixel-by-pixel basis. However, it is important to note that
on a pixel-by-pixel basis. However, it is important to note that