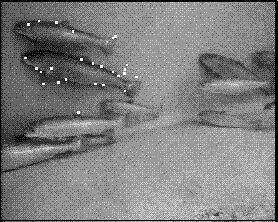
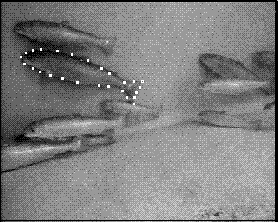
Fitting 3D point distribution models of fish to stereo images
Nigel J.B. McFarlane and Robin D. Tillett
Silsoe Research Institute
Wrest Park, Silsoe, Bedford, MK45 4HS, UK
nigel.mcfarlane@bbsrc.ac.uk
Abstract
Stereo images of Atlantic salmon (
Salmo salar
) in a tank were captured from a pair of calibrated underwater cameras.
A 3D point distribution model (PDM) was constructed from an example set
of 25 unoccluded fish, representing the means and variances of the
shape, size, position and rotation of the fish within the example set.
The PDM was fitted to test fish by minimising an energy function, which
was based on probability distributions. The minimisation was an iterated
two-step method in which edges were selected for magnitude, direction
and proximity to the model, and the model was then fitted to the edges.
A search strategy was devised for locating the edges in 3D. The
algorithm was tested on 26 unoccluded fish, and converged successfully
in 19 of the cases.
1 Introduction
Accurate monitoring of fish size is essential in aquaculture, because it affects the quantity of food required and the timing of grading and harvesting operations. At present, this is performed by removing a sample of fish from the water, but this has been shown to be inaccurate, can cause stress and damage to the fish, and may be impossible in bad weather [1]. The masses of individual Atlantic salmon ( Salmo salar ) have been measured to within ±9% from underwater stereo images [1], showing the potential of image analysis as a non-invasive technique for the continuous monitoring of fish stocks.
Point Distribution Models (PDM's) [2], consisting of a set of landmark points and their modes of variation, are a convenient and trainable method of modelling the variable shape of biological objects. They are especially attractive for representing fish shape because the positions of landmarks have already been correlated with the masses of salmon [3], although in this case the landmarks were measured by hand on anaesthetised fish.
The aim of this work was to create a 3-dimensional PDM of a salmon by training the model on landmarks placed on stereo images of fish and to develop an image analysis algorithm for fitting the PDM automatically to images of fish in a separate test set.
The images used in this work presented considerable problems for any algorithm attempting to locate the edges of the fish, because of the large number of false edges produced by shadows, highlights, neighbouring fish and patterns on the fish surface. The incorrect edges were often similar in magnitude, direction and length to the correct ones, and could occur very close to the true edges.
Methods for fitting models to image data include those which measure the image only at the current positions of the template [4], such as snakes [5,6,7,8], which attempt to slide into position by following local image gradients. This approach was inadequate in this application, because the initial landmark positions were, in general, too far away from their correct positions for the correct edges to have any influence, even if the model was initialized exactly in the centre of the fish. Stochastic methods such as Markov chain Monte Carlo (MCMC) [9] escape from local minima and featureless parts of the image by random jumps, but such methods tend to be slow. In a related project [10], a 2D PDM was fitted to images of fish using the MCMC technique. When fitting PDM's, a common approach is to first locate the edges by thresholding and then to attract the landmarks to their nearest edges [11]. This allows the PDM to be pulled by more distant edges, but the assumption that the correct edge was the nearest was not always valid in this application. In this work, a fitting method was developed in which the edges were located by thresholding, but the PDM was attracted not just to the nearest, but to edges selected by a combination of edge strength and proximity, allowing the PDM to "see" stronger edges beyond weaker but closer ones.
One of the problems of fitting models such as snakes is that the energy
functions which are minimised contain constants which need to be "tuned"
to the application, and which are difficult to estimate [12,13]. In this
work, the constants in the energy function were all related to
probability distributions, and were easily learnable or estimated.
2 Description of images
Stereo images were captured of Atlantic salmon (
Salmo salar
) in a tank, using a pair of underwater cameras [1]. The cameras were
positioned above and below each other, and were calibrated from a
submerged grid of known dimensions by Tsai's method
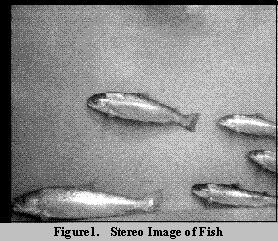
[14]. Figure 1 shows a typical pair of images. The dimensions of the
images were 320 x 256 pixels. A displacement of one pixel in image
coordinates corresponded to a real-world displacement of approximately 2
to 5 mm over the range of depths occupied by the fish. The images were
divided into 18 training images, which were used for learning the model
of the fish shape, and 18 test images, which were used for testing the
algorithms.
3 Point Distribution Model
In this work, the shape of a fish was defined as the shape, size, orientation and position of its self-occluding boundary, or outline, as viewed from 2 directions by the stereo cameras. In defining the shape in this way, it was assumed that each fish was approximately flat in cross-section, and hence that the points perceived to be on the self-occluding boundary were the same in both cameras.
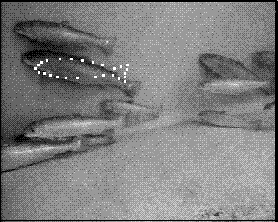
The shape was modelled by a point distribution model (PDM) [2] consisting of 26 landmark points. Figure 2 shows a stereo image pair with the landmarks indicated. Some of the landmarks corresponded to physical features of the fish, such as the tip of the tail or the junction of a fin with the body. Others were added to fill in the gaps along featureless parts of the shape. All of the landmarks were points on the self-occluding boundary, because there were so few landmarks on the surface of the fish, but further work might include features such as the eye or the gill slit in the model. In this work, the fins, which were not always visible, were not included as part of the shape.
The training set images contained 25 fish which were suitable for training the PDM, in that they were unoccluded in both stereo images, and oriented side-on to the cameras. For each fish in the training set, the landmarks were placed by hand in both images of the stereo pair. Then the 2 sets of image coordinates were used to calculate the 3D positions of the landmarks in world coordinates.
The 25 example fish shapes were then normalised to the same scale, rotation and translation. The translation parameters, x 0 , y 0 and z 0 , were respectively the mean x, y and z real-world positions of the points; the rotation parameters, , and , were respectively the Euler angles [15] describing the roll, pitch and yaw of the principal axes; and the scale parameter, s, was the r.m.s. distance of the shape points from the centre (x 0 ,y 0 ,z 0 ). Reflection was not included in the model, because the fish in this work were all swimming in the same direction.
The values of the parameters for each shape were recorded, and each shape was then normalised such that x 0 , y 0 and z 0 were all zero, , and were all zero, and s was unity. This omitted the minimisation step of Cootes, in which all the shapes in the training set were translated, rotated and scaled so as to optimise their fit to the collective mean shape. In this application, the principal axes of the shapes were well-defined enough that there was little difference between the parameters derived by direct calculation or by optimised fit, but the shapes produced by the optimal fit were not completely normalised, having some residual variation in scale and rotation. In this application, the variances in scale and rotation were potentially of interest, so the direct calculation, which separated the variations in scale, rotation and translation entirely from the variations in pure shape, was preferred.
The modes of variation of the normalised shapes were then calculated, using principal component analysis, and arranged in order of descending eigenvalues. The eigenvectors of the covariance matrix represented the principal modes of variation of the shape, and the eigenvalues the variances along these modes. The shape model used in this work was thus given by:

where u = (x 1 ...x n y 1 ...y n z 1 ...z n ) T , u m was the mean normalised shape, P was the 3n x n t matrix of the n t eigenvectors with the largest eigenvalues, and b was the vector consisting of the n t components of shape resolved along these eigenvectors; and

where x was the calculated shape, in the form of a 3 x n matrix, x was the 3 x n matrix of coordinates corresponding to u , R (,,), was the Euler rotation matrix, and x 0 was the translation vector (x 0 y 0 z 0 ) T . In this work, the value of n t was 6, which was a fairly arbitrary cut-off which assumed that all but the first 6 modes of variation were negligible. Hence the shape model was described by 13 parameters: 6 modes of shape variation and 7 parameters of scale, rotation and translation.
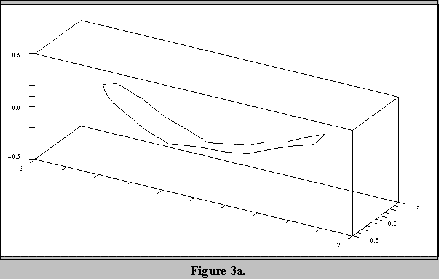
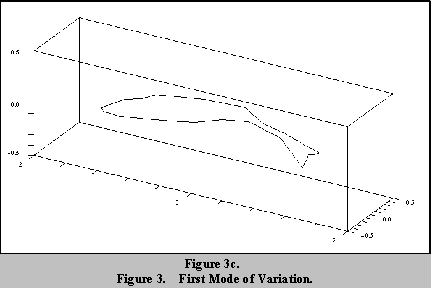
Figures 3a to 3c show the first mode of variation of the fish shape.
Figures 3a and 3c show the shape modified by plus and minus 2 standard
deviations about the mean shape
u
m
, shown in figure 3b.
4 Energy functions
The PDM was fitted to the test fish by minimising an energy function. The energy function consisted of three components: E pdm ( p , b ) was the energy of the PDM position and shape, where p was the vector comprising the 7 components of scale, rotation and translation, and b was the vector comprising the 6 components of shape variation; E im ( e ) was the energy of the 2 stereo images at the world position e of a candidate edge; and E resid (d[ x , e ]) was the energy due to the residual distance d[ x , e ] between the landmark at x and the corresponding candidate edge point at e .
In this work, the energy of an event occurring, for example, a particular set of values of p and b , was minus the log likelihood of the event. The more probable the event, the lower the energy. E pdm was simple to calculate, since the model described the components as varying according to independent Gaussian distributions. Hence, E pdm was given by:
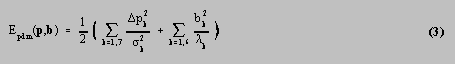
where p k was the deviation from the mean of position parameter p k , k was the standard deviation of p k , and k was the kth eigenvalue of the PDM, equal to the variance of b k . The additive constants have been ignored throughout this work. E resid was similarly easy to calculate, but in this case, a Gaussian distribution of likelihood vs distance was not suitable, because of the presence of outlier points. The edge candidates were sometimes incorrect, and occurred at greater distances from their corresponding landmarks than would have been allowed for by a Gaussian distribution. To avoid a small number of outliers exerting too much influence on the overall fit of the PDM to the points, a robust energy function was used, corresponding to the Cauchy distribution [16]. This was given by

where d 0 was a length constant analogous to the standard deviations in Eqn 3.
Finally, the image energy E im ( e ) was a function of the edge magnitude and direction at the image coordinates corresponding to the world point e . All of the landmark points in this work corresponded to edge features, and therefore needed to be fitted to edges in the images. An edge was assumed to be better, the larger the magnitude of the image gradient, and the more closely its direction matched that of the normal to the PDM at the corresponding landmark point. The absolute grey levels were not used, because of the danger of learning features which were only applicable to the current lighting conditions and camera angles. Knowledge as to whether the fish were lighter or darker than the background was also not used, because this tended to vary from point to point around each fish, and hence required a model of the grey level pattern on the body of the fish. Such models have been used to model the grey level patterns on pigs [17,18] or the colours of leaves [19], but the grey level patterns in the images used here included highlights and shadows which were specific to the imaging configuration. The image energy at world point e was given by
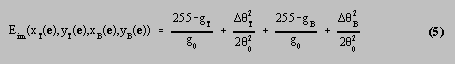
where x
T
, y
T
, x
B
and y
B
were the coordinates in the top and bottom stereo images, g
T
and g
B
were the magnitudes of the image gradients in the images, and
T
and
B
were the differences between the observed gradient directions and the
normals to the PDM. The gradient magnitudes and directions were
calculated for the images using a Sobel operator. The direction normal
to the PDM projected into an image, at a particular landmark, was the
normal to the vector drawn through the two neighbouring landmark points.
An angle was regarded as the same as + for calculating the angular
differences, because it was possible for parts of the fish to be
brighter or darker than the background, and therefore no distinction was
made between gradient vectors pointing inwards or outwards from the
fish. The constant
0
was the standard deviation of the observed directions about the PDM
normals, assuming a Gaussian distribution. The distribution of the
gradient magnitude had no single preferred value, so a linear energy
function was used for simplicity. The constant g
0
was a measure of the expected magnitude of the correct edges compared to
that of the image noise.
5 Fitting algorithm
The energies described in section 4 were combined into a total energy function E given by
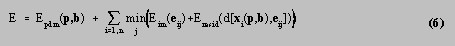
where x i (p,b) was the position of the ith landmark point and e ij was the position of the jth edge candidate corresponding to the ith landmark. The method used to fit the PDM to the fish was an iterated two-step method.
In step 1, the PDM was held fixed, whilst a set of candidate edges e ij was identified for each landmark point x i . In each image, a search was performed along the normals to the landmarks, recording edges for which the magnitudes and directions were within thresholded limits. The thresholds were not essential for the algorithm to work, but reduced the processing time required by removing obvious non-edges at an early stage. At this point, the edge candidates for each landmark consisted of two lists of 2D image coordinates, which were combined by converting every pair of points (x T ,y T ) and (x B ,y B ) into a world point e ij . In general, the normal search directions in the images did not coincide with epipolar lines, so the reprojection of e ij into the images was a point close to, but no longer the same as, (x T ,y T ) and (x B ,y B ). This was a potential problem, because the image energy would be measured at image points different from those at which the original edges had been recorded. However, if it was assumed that the edges were approximately straight over the distances involved, then if (x T ,y T ) and (x B ,y B ) were points on the same edge, the reprojected points should also fall on the edge. Having obtained the candidate edges e ij , the function

was then minimised over j for each landmark, so that each landmark x i was associated with one edge point e i .
In step 2, the best edge candidates were held fixed whilst the PDM was fitted to them by minimising the function
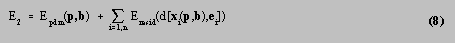
over all components of p and b . Powell's method [16] was used for the minimisation of E 2 .
Steps 1 and 2 were iterated several times.
At the start of the iterations, it was not known how close the PDM was to its correct position, but at the end, assuming that the PDM has converged properly, the landmarks were expected to be close to their corresponding image edges. Hence it was reasonable to "anneal" Eqn 4 by gradually reducing the distance d 0 on each iteration, and hence changing the relative weight given to the strength and the distance of the edge candidates. The value of d 0 on iteration k was given by

where d
00
was the initial value and µ was an annealing rate constant.
6 Results
The constants which were not learned from training the PDM were set to
the following values:
g 0 = 20 grey levels per pixel
0 = 0.175 rad
d 00 = 50.0 mm
µ = 1.2
The fitting algorithm was tested on the 26 unoccluded fish from the test images. In each case, the PDM parameters were set to their mean training set values, and the PDM was then moved by hand such that its translated position was close to the centre of the test fish. The scale, rotation and shape were not changed. The algorithm described in sections 4 and 5 was then executed for 34 iterations. Figure 4 shows the initial position of the PDM in a stereo pair of test images, figure 5 shows the best candidate edges detected from the initial position, and figure 6 shows the final position of the PDM.
The success of the algorithm in converging on the fish was judged by eye. The PDM was judged to have converged on the fish if most of the landmarks were on the occluding boundary of the fish in both images. In 19 out of the 26 tests, the PDM converged successfully, and in 5 of these cases, all of the landmarks were positioned correctly. Complete failure to converge could usually be attributed to one of three reasons:
The PDM was pulled out of position by attempting to fit to the edges of a neighbouring fish.
The orientation of the test fish was so different from that of the initial PDM that the edges of the fish were ignored due to not being in an appropriate direction.
The fish were much smaller than the initial PDM. This may have been due to the limits placed on the edge searching, which prevented edges being detected too far away in the inward direction. This limit was supposed to prevent the opposite sides of the PDM from pursuing the same edges, but it may also have made it difficult for the PDM to shrink.
Imperfect convergence almost always occurred in the tail region. The tail presented many more problems for a converging template than the head, including:
The 2 tips of the tail were not really edges at all, but corners. A search along a single line would easily miss such a point. A strong case could be made for labelling such landmarks as corners in the PDM, and using a different search strategy for finding them.
The end of the tail was often a very weak edge. This was compounded by the presence of a strong edge just inside the tail, where the body of the fish ended and the tail fin began. This edge often attracted the PDM, preventing it from converging on the desired edge.
The PDM sometimes failed to extend to the end of the tail, when despite locating the correct edges, the model would not move towards the points. It appeared that once the landmarks along the body of the fish had been located, the PDM had difficulty sliding parallel to the body. This may have been due to the fact that the landmarks could only "see" edges normal to the body, which produced an unnecessary resistance to moving in any direction away from the located points, including the parallel direction. The small number of tail points could not move the PDM against the resistance of large numbers of landmarks on the body. This problem might be solved by changing the energy E resid such that it does not penalise movement parallel to edges, or by allowing landmarks to be attracted to the edges found by their neighbours.
The non-convex shape and small size of the tail meant that the "inward limit" of the edge search could prevent some points being seen at all, unless the tail was already close to its correct position. This, combined with the other difficulties in locating the correct edges, made the tail easily attracted out of position by the edges of neighbouring fish.
The PDM itself, limited to 6 modes of variation, had no difficulty in
fitting to the shapes of the fishes, except in the case of one test
fish, in which it was suspected that the failure of the PDM to stretch
to the tail was due to the fish being unusually thin. However, the fish
in the test images were often the same individuals as in the example
images, and further work is required to test the PDM on a set of
different fish. The training set was quite small, and appeared to
contain more large fish than the test set, so further work is required
to train the PDM on more fish.
7 Further work
Possible improvements to the fitting algorithm include the use of landmarks other than edges, such as corner points or surface features, and modifying the algorithm to allow easier movement of the PDM parallel to edges. Aspects of the work requiring more extensive testing include the ability of the 6-mode PDM to represent the salmon and the effectiveness of the search procedure in locating the edges in stereo. Quantitative measurements of the fitting accuracy, and an assessment of how close to the fish the initial PDM had to be to converge, are required.
In the application area, further work is planned in relating the size of
the fish, as measured from the image, to the mass. This might entail
modifications to the PDM to reflect measurements known to correlate with
the mass.
8 Conclusions
The point distribution model successfully modelled the shapes of the fish in 3D with 6 modes of variation.
The constants in the fitting algorithm were all related to probability distributions of shape, grey level, direction and distance, so their magnitudes were easily measured or estimated.
The PDM converged on the fish in 73% of the cases, with minor problems in locating the tail accurately. This was despite a great deal of image noise in the form of shadows, neighbouring fish, and shading patterns on the fish themselves.
The two step algorithm allowed the PDM to locate and move towards edges which were a long distance away. In selecting the edge points to move towards, a combination of edge strength and distance was used, which enabled the PDM to locate the best, rather than just the nearest edges.
The method of locating edges in stereo by searching along normals to the shape model in each image, converting each pair of points to world coordinates, and testing at the reprojected image points, worked adequately, but needs further assessment.
Further work is required in improving the ability of the algorithm to locate corners and to slide parallel to edges.
Further work is planned in relating the image measurements to the mass
of the fish.
Acknowledgement
The authors would like to thank the Institute of Aquaculture at the
University of Stirling for providing access to their images.
References
[1] Beddow, T.A., Ross, L.G. and Marchant, J.A. Predicting salmon biomass remotely using a digital technique. Aquaculture 146 (1996), 189-203
[2] Cootes, T.F. et al. Training models of shape from sets of examples. Proc 3rd British Machine Vision Conf., Leeds, UK, 22-24 Sept 1992, 9-18.
[3] Beddow, T.A. and Ross, L.G. Predicting biomass of Atlantic salmon from morphometric lateral measurements. Journal of fish biology 49, 3 (1996) 469-482
[4] Staib, L.H. and Duncan, J.S. Boundary finding with parametrically deformable models. IEEE trans pattern analysis and machine intelligence, 14, 11 (1992)
[5] Kass, M. et al. Snakes: active contour models. Int. journal of computer vision , 1 (1988) 321-331
[6] Waite, J.B. and Welsh, W.J. An application of active contour models to head boundary location. Proc 1st British Machine Vision Conf ., Oxford, UK, 24-27 Sept 1990, 407- 412.
[7] Radeva, P. et al. A snake for model-based segmentation. Proc 5th Int. Conf. on Computer Vision , Cambridge, USA, 20-23 June 1995, Ch. 162, 816-821.
[8] Gunn, S.R. and Nixon, S.M. A robust snake implementation; a dual active contour. IEEE trans pattern analysis and machine intelligence , 19, 1 (1997)
[9] Mardia, K.V. The art and science of Bayesian object recognition. Int. conf. on image fusion and shape variability techniques , Leeds, UK, 3-5 July, 1996
[10] de Souza, K.M.A., Kent, J.T. and Mardia, K.V. Estimation of objects in highly variable images using Markov chain Monte Carlo. Submitted to the British Machine Vision Conference, BMVC 1997.
[11] Cootes, T.F. and Taylor, C.J. Data driven refinement of active shape model search. Proc 7th British Machine Vision Conf. , Edinburgh, UK, 9-12 Sept 1996, 383-392.
[12] Gang, X. et al. Robust active contours with insensitive parameters. Pattern recognition , 7, (1994), 879-884.
[13] Samadani, R. Adaptive snakes: control of damping and material parameters. Proc. conf on geometric methods in computer vision , San Diego, USA, 25-26 July 1991.
[14] Tsai, R.Y. An efficient and accurate camera calibration technique for 3D vision. Proc. IEEE conf on computer vision and pattern recognition . Miami Beach, USA, 22-26 June 1986.
[15] Goldstein, H.G., Classical mechanics , 2 ed. (1980), Addison-Wesley, ISBN 0-201- 02969-3
[16] Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. Numerical Recipes in C , 2 ed. (1995), Cambridge U.P. ISBN 0 521 43108 5
[17] Onyango, C.M., Marchant, J.A. and Ruff, B.P. model based location of pigs in scenes. Computers and electronics in agriculture , 12 (1995), 261-273
[18] Onyango, C.M. and Marchant, J.A. modelling grey level surfaces using three- dimensional point distribution models. Image and vision computing , 14 (1996), 733-739
[19] Onyango, C.M. and Marchant, J.A. Flexible colour point distribution
models.
Image and vision computing
, 14 (1996) 703-708